티스토리 뷰
영리한 프로그래밍을 위한 알고리즘 강좌 '(링크)와 '쉽게 배우는 알고리즘 관계 중심의 사고법 - 문병로' 참조
5-3. Red-Black Tree 03 - DELETE, FIXUP
DELETE
보통의 BST에서처럼 DELETE한다.
실제로 삭제된 노드 y가 red였으면 종료
y가 black이었을 경우 RB-DELETE-FIXUP을 호출한다.
pesudo code
01 : 삭제할 노드 z의 왼쪽, 오른쪽 자식이 NULL이 아니라면 즉, 자식이 없다면
02 : y에 z를 저장하고
03 : 자식이 있다면, z의 Successor를 찾아서 y에 저장한다. BST에서 Successor찾는 과정과 동일
04 : 01-03과정을 거치면 y는 자식이 하나이거나 없다. Successor는 자식노드가 두 개일 수 없다. y의 왼쪽 자식이 null이 아니라면
05 : y의 왼쪽 자식을 x로
06 : 그렇지 않다면, y의 오른쪽 자식을 x로 저장한다.
07 : 그다음 y의 부모를 x의 부모로 설정한다.
08 : 만약, y의 부모가 NULL이라면
09 : x를 트리의 root로 설정한다.
10 : y의 부모노드가 NULL이 아니고, y가 y의 부모의 왼쪽 자식노드라면
11 : 저장된 x를 y의 부모의 왼쪽 자식노드로 설정한다.
12 : y가 y의 부모의 오른쪽 자식노드라면, 저장된 x를 부모노드의 오른쪽 자식으로 설정한다. 여기까지가 실제로 노드를 삭제하는 작업이다.
13 : 삭제하려는 노드 대신 Successor를 삭제한 경우 y와 z가 다르다. 따라서 Successor y노드의 데이터를 카피해주는 작업이 필요하다.
14 - 15 : y의 데이터들을 z노드로 copy해주는 작업
15번 라인까지의 작업은 BST의 DELETE작업이다. 아래의 3줄은 RBT의 경우에 해줘야하는 연산이다.
삭제한 노드 y가 red 노드 였다면, RBT의 규칙에 위반 되지 않는다.
16 : 삭제한 노드 y가 BLACK 노드일 경우
삭제한 노드가 루트노드인데, 그 자식인 레드노드가 올라와서 루트가 된 경우,
중간의 black노드가 삭제되억서 red - red 위반이 생긴 경우,
트리를 따라 내려가면서 black노드의 갯수가 일치하지 않는 경우가 생길 수 있다.
17 : 문제들을 해결하기 위해 RBT-DELETE-FIXUP(T, x)를 통해서 트리의 규칙을 만족하기 위한 작업을 한다. y의 자식인 x를 넘겨서 정렬한다.
18 : 삭제된 노드 y를 반환한다.
RB-DELETE(T, z)
01 if left[z] = nil[T] or right[z] = nil[T]
02 then y <- z
03 else y <- TREE-SUCCESSOR(z)
04 if left[y] != nil[T]
05 then x <- left[y]
06 else x <- right[y]
07 p[x] <- p[y]
08 if p[y] = nil[T]
09 then root[T] <- x
10 else if y = left[p[y]]
11 then left[p[y]] <- x
12 else right[p[y]] <- x
13 if y != z
14 then key[z] <- key[y]
15 copy y's satellite data into z
16 if color[y] = BLACK
17 then RB-DELETE-FIXUP(T, x)
18 return y RB-DELETE-FIXUP(T, x)
x가 NIL 노드일 수도 있다. 그리고 x가 red일 경우 쉽게 해결할 수 있다. 이 두가지를 기억한다. 실제로 DELETE에서 문제는 x가 BLACK인 경우다.
위반 될 수 있는 규칙 정리
각 노드는 red 혹은 black이다.
문제 없음
루트노드는 black이다.
y가 루트였고, x가 red인 경우 위반된다. 하지만, 심각한 문제는 아니다.
모든 리프노드(즉, NIL 노드)는 black이다.
문제 없음
red노드의 자식노드들은 전부 black이다.(즉, red노드는 연속되어 등장하지 않고)
p[y]와 x가 모두 red일 경우 위반
x가 레드인 경우 red를 black으로 바꾸어 주면 되기 때문에 심각한 문제는 아니다.
모든 노드에 대해서 그 노드로 부터 자손인 리프노드에 이르는 모든 경로에는 동일한 개수의 black노드가 존재한다.
원래 y를 포함했던 모든 경로는 이제 black노드가 하나 부족하다.
노드 x에 "extra black"을 부여해서 일단 조건5를 만족시킨다. 색을 두개 가지고 있게 하는 임시 방법이다.
그렇게 되면 노드 x는 "double black" 혹은 "red & black"이 된다. 앞으로 해결해야하는 문제가 이 것을 블랙노드로 바꾸는 것이다.
문제 해결 아이디어
Extra black을 순차적으로 트리의 위쪽으로 올려보낸다. x의 부모 가 double black이 되는 식으로.
x가 red & black 상태가 되면 그냥 black노드로 만들고 끝낸다.
x가 루트가 되는 순간까지 올라가면 그냥 extra black을 제거한다.
Loop Invariant(루프를 돌면서 변하지 않고 유지되는 조건)
x는 루트가 아닌 double-black노드
w는 x의 형제노드
w는 NIL 노드가 될수 없음 (아니면 x의 부모에 대해 조건5가 위반 됨.)
문제 정의
DELETE의 경우 8가지 case로 분류할 수 있다. INSERT와 마찬가지로 1,2,3,4와 5,6,7,8은 대칭이다.
Case 1,2,3,4 : x가 부모의 왼쪽 자식노드인 경우
x는 double black노드이거나, NIL 노드 일수도 있다.
x의 형제노드인 w노드는 반드시 존재하고, NIL일 수는 없다.
x는 자신의 부모의 왼쪽 자식이다.
Case 5,6,7,8 : x가 부모의 오른쪽 자식노드인 경우
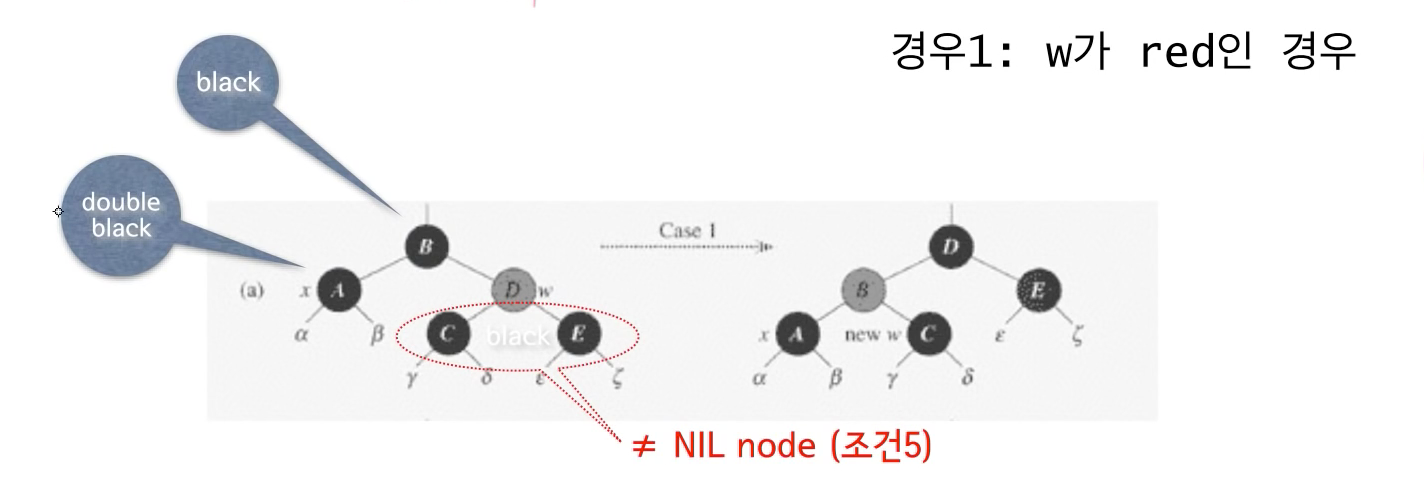
Case 1 - x의 형제노드 w가 RED인 경우
Case 1,2,3,4의 공통 조건에 해당하며, 케이스 1인 경우는
x의 형제노드 w가 RED인 경우이다. 이 경우는 자식노드가 NIL일 수 없고, BLACK 노드이다.
이 상황에서 문제를 해결하기 위해,
w를 BLACK으로 p[x]를 RED로 바꾼 뒤
p[x]에 대해서 left-rotation을 적용한다. x는 여전히 double-black 노드를 가지고 있다.
x의 새로운 형제노드는 원래 w의 자식노드이다.
따라서, 새로운 w노드는 black노드이다. 이 경우 Case 2, 3, 4로 넘어가게 된다.
정리를 하면, Case1의 경우 x의 부모 노드에 대해서 left-rotation을 적용하면, 새로운 w노드가 red가 아닌 black이 되는 상황이라서 Case 2, 3, 4로 넘어가게 된다.
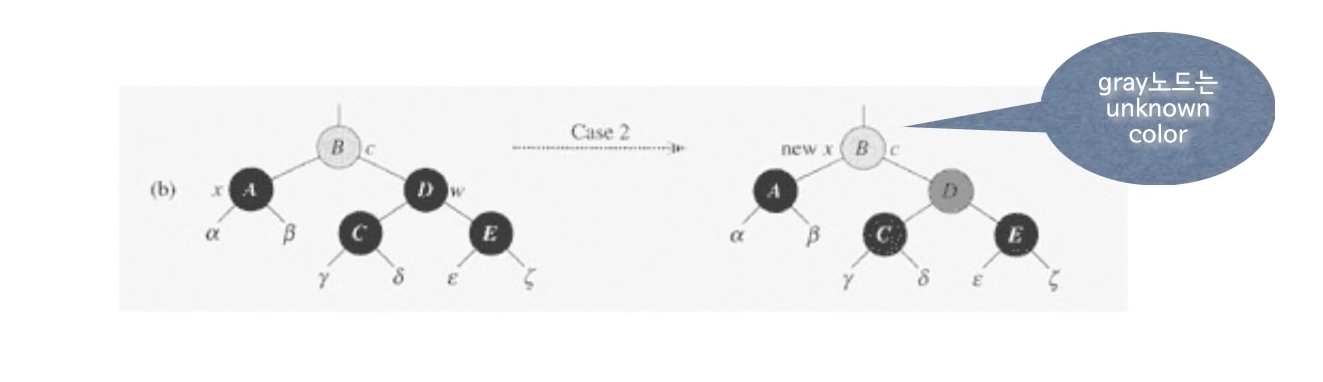
Case 2 - w는 BLACK, w의 자식들도 BLACK인 경우
case 2, 3, 4의 경우 x의 형제노드 w가 BLACK인 경우이다. 이 중에서 w의 자식들도 모두 BLACK인 경우가 Case 2에 해당한다.
이 경우, x와 w가 모두 블랙이므로 부모인 B노드는 RED 일수도 있고, BLACK 일수도 있다.
현재 x는 double black 노드이고, w는 black 노드이다.
이 상황에서 x와 w로부터 black을 하나씩 뺏어서, 부모노드에게 준다.
결과적으로 x는 extra black이 하나 없어졌으므로 BLACK노드가 됐고, w는 black을 뺏겼으므로 RED노드가 된다.
다음으로 p[x]에게 extra-black 노드를 준다. 이렇게 하면, 트리의 위에서 부터 내려오면서 유지하던 BLACK노드의 갯수가 유지 된다.
만약 p[x]가 RED였다면, 위에서 설명했던 것처럼 red & black을 가지고 있는 노드를 BLACK노드로 만들고 끝내면 되고, p[x]가 BLACK이었다면 p[x]를 새로운 x로 해서 계속한다.
만약 Case1에서 Case2에 도달한 경우면 p[x]는 red였고, 따라서 새로운 x는 red & black이 되어서 종료된다.
하지만 Case2로 바로 온 경우에 p[x]가 원래 BLACK이었다면, p[x]가 double black이 되므로 반복해서 문제를 해결해야 할 수도 있다.(뒤에서 설명) 다만, extra-black이 한 level 올라갔다.
Case 3 - w는 BLACK, w의 왼쪽자식이 RED
w를 RED로, w의 왼쪽자식노드를 BLACK으로 바꾼다.
w에 대해서 right-rotation을 적용한다.
x의 새로운 형제 w는 오른자식이 RED이다. 이것은 경우 4에 해당한다.

Case 4 - w는 BLACK, w의 오른쪽자식이 RED
w의 색을 현재 p[x]의 색으로(unknown color)
p[x]를 BLACK으로, w의 오른자식을 BLACK으로 바꾼다.
p[x]에 대해서 left-rotation을 적용한다.
x의 extra-black을 제거하고 종료한다.
이렇게 되면, double-black노드가 없어졌음에도 불구하고, 기존의 A노드를 지나는 블랙노드의 갯수가 로테이션 전과 똑같아 진다. 그리고 나머지 C와 E를 지나는 블랙노드의 갯수도 기존과 동일하게 유지된다.

RB DELETE FIXUP pesudo code
레드블랙트리에서 실제로 삭제한 노드는 y이다. 삭제한 노드 y의 자식인 x를 넘겨주면서 Delete Fixup을 하게 된다.
01 : 만약 x가 루트노드이거나, x가 레드노드라면 While문을 빠져나가서 x를 BLACK으로 만들어주고 종료하면 된다.
02 : While문 안에서는 크게 둘로 나뉘어지게 된다. 만약 x가 x의 부모노드의 왼쪽 자식이라면 Case 1, 2, 3, 4에 해당하며 부모노드의 오른쪽 자식이라면 Case 5, 6, 7, 8에 해당한다.
03 : 노드 x의 형제노드인 w를 저장한다. x가 p[x]의 왼쪽 자식이므로, w는 오른쪽 자식 노드가 된다.
04 : 형제 노드인 w노드가 RED인 경우가 Case 1에 해당한다.
05 - 08 : Case1의 경우 w노드를 BLACK으로 만들고, p[x]노드를 RED로 만든 다음, p[x]를 기준으로 LEFT-ROTATE한다. 새로운 w는 p[x]의 right가 되므로 새로 저장한다. 이때, 새로운 w노드는 BLACK 이므로(p[x]가 RED로 변경됨) 다시 While문으로 들어왔을 때, Case2, 3, 4로 가게 된다.
09 : Case 2, 3, 4를 구분하게 된다. w의 왼쪽, 오른쪽 자식노드가 둘다 BLACK인 경우 Case2에 해당한다.
10 - 11 : 위에서 학습한 내용과 같이 w와 x로 부터 black을 하나씩 뺏어서 부모 노드에게 전달한다. 그렇게 하기 위해서 w는 RED노드가 되고, p[x]를 x로 만들어 준다. p[x]가 RED였다면 다시 While문을 돌지 않고 x를 RED로 만든 뒤에 종료하면 되고, p[x]가 BLACK이었다면 x를 p[x]로 놓고 double-black 노드가 된 x를 다시 반복해서 처리해주면 된다.
12 : w의 오른쪽 자식이 BLACK이고, 왼쪽 자식이 RED인 경우 Case 3에 해당한다.
13 - 16 : RIGHT-ROTATE의 대상인 두 노드의 색을 exchange 하고(w를 RED로, w의 왼쪽 자식노드를 BLACK으로 바꾸고), w를 기준으로 RIGHT-ROTATE 한다. 이렇게 되면 w는 p[x]의 새로운 오른쪽 자식노드가 되고, 그것의 색은 RED이다. 그리고 Case 4로 바로 넘어 간다.
17 - 20 : LEFT-ROTATE의 대상인 두 노드의 색을 exchange 하고(w의 색을 p[x]의 색으로, p[x]를 BLACK으로) w의 오른쪽 자식노드의 색을 BLACK으로 바꾼다. 그 다음 p[x]를 기준으로 LEFT-ROTATE를 수행한다.
21 : x라는 포인터 변수를 root[T]로 변경하여 Case 4가 끝나면 while문이 종료되도록 한다. 실제 트리에는 변화가 없다. 트리의 루트가 변한것도 아니다.
22 : Case 5, 6, 7, 8을 대칭적으로 처리한다.
x가 p[x]의 오른쪽 자식인 경우이다.
23 : 트리의 루트의 색을 BLACK으로 변경하는 것은 언제 해도 문제가 되지 않는다.
RB-DELETE-FIXUP(T, x)
01 while x != root[T] and color[x] = BLACK
02 do if x = left[p[x]]
03 then w <- right[p[x]]
04 if color[w] = RED
05 then color[w] <- BLACK // Case1
06 color[p[x]] <- RED // Case1
07 LEFT-ROTATE(T, p[x]) // Case1
08 w <- right[p[x]] // Case1
09 if color[left[w]] = BLACK and color[right[w]] = BLACK
10 then color[w] <- RED // Case2
11 x <- p[x] // Case2
12 else if color[right[w]] = BLACK
13 then color[left[w]] <- BLACK // Case3
14 color[w] <- RED // Case3
15 RIGHT-ROTATE(T, w) // Case3
16 w <- right[p[x]] // Case3
17 color[w] <- color[p[x]] // Case4
18 color[p[x]] <- BLACK // Case4
19 color[right[w]] <- BLACK // Case4
20 LEFT-ROTATE(T, p[x]) // Case4
21 x <- root[T] // Case4
22 else (same as then clause with "right" and "left" exchanged)
23 color[x] <- BLACK 
RB DELETE FIXUP - Case 흐름
전체 케이스는 1 - 8의 경우이지만 1,2,3,4와 5,6,7,8은 대칭적인 관계이므로 1,2,3,4에 대해서만 그린 흐름이다.
처음부터 Case 4의 경우에 해당하면, left-rotation과 extra-black노드를 뺏는 것으로 바로 Case가 종료가 된다.
Case 3으로 가면 right-rotation으로 Case 3을 처리하고, Case 4로 상황이 바뀐다.
Case 1으로 가면, Case 1이 해결되고 Case 2, 3, 4로 넘어간다.
처음부터 Case 2로 가는 경우에는 바로 종료되지 않고 차이가 있다.
Case 2가 반복되는 동안 extra-black노드는 계속해서 트리의 위로 이동한다. 이 상황에서 Case 1, 3, 4로 이동하게 되면 흐름에 따라 2 step 이내에 종료되게 된다.
물론, Case 5, 6, 7, 8로 넘어가서 Case 2의 대칭인 Case 6의 경우와 왔다갔다 할 수도 있고, Case 5, 7, 8로 이동하여 끝날 수도 있다.

시간복잡도
BST에서의 DELETE : O(logn)
RB-DELETE-FIXUP : O(logn)
가장 최악의 경우인 Case2와 6이 반복되는 경우에도 최대 트리의 높이만큼 실행된다.
따라서, DELETE와 FIXUP을 합쳐도 O(logn)의 시간이 된다.
'ICT Eng > Algorithm' 카테고리의 다른 글
| [Algorithm] 6-2. Hash 함수, Hashing in Java (0) | 2018.04.17 |
|---|---|
| [Algorithm] 6-1. Hashing 개요 - Chaining, Open Addressing, SUHA (0) | 2018.04.17 |
| [Algorithm] 5-2. Red Black Tree 02 - INSERT, FIXUP 연산 (0) | 2018.03.29 |
| [Algorithm] 5-1. Red Black Tree 01 - 개요 (0) | 2018.03.29 |
| [Algorithm] 4-2. Binary Search Tree - 이진탐색트리 (1) | 2018.02.09 |
- Total
- Today
- Yesterday
- ORM
- AWS
- 자바
- github
- Vue.js
- 젠킨스
- 무선통신소프트웨어연구실
- vuex
- 스프링부트
- JPA
- 한밭대학교
- vuejs
- IT융합인력양성사업단
- 순환
- 인프런
- 한밭이글스
- Java
- 알고리즘
- Recursion
- Wisoft
- 레드블랙트리
- Raspberry Pi
- 라즈베리파이
- 시간복잡도
- 정렬
- springboot
- RBT
- Algorithm
- Spring
- Spring Boot
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
