티스토리 뷰
[Algorithm] 6-1. Hashing 개요 - Chaining, Open Addressing, SUHA
nroo 2018. 4. 17. 02:48영리한 프로그래밍을 위한 알고리즘 강좌 '(링크)와 '쉽게 배우는 알고리즘 관계 중심의 사고법 - 문병로' 참조
6-1. Hashing 01 - 개요
Hash Table
탐색과 삽입, 삭제를 지원하는 자료구조를 dynamic set이라고 부른다.
4장에서는 검색트리를 가지고 dynamic set을 구현했고, 또다른 한가지 구현 방법이 Hashing을 이용하는 것이다.
해시 테이블은 dynamic set을 구현하는 효과적인 방법의 하나이다.
"적절한 가정"하에서 평균 탐색, 삽입, 삭제시간 O(1)
보통 최악의 경우 O(n)
해시 함수(hash function) h를 사용하여 키 k를 T[h(k)]에 저장
h : U -> {0, 1, 2, … , m-1}
여기서 m은 테이블의 크기, U는 모든 가능한 키들의 집합
키 k가 h(k)로 해싱되었다고 말한다.
즉, h() 해시 함수는 각 키에 대한 해시함수값을 그 키를 저장할 배열 인덱스로 사용한다.

해시 함수의 예
모든 키들을 자연수라고 가정(어떤 데이터든지 자연수로 해석하는 것이 가능하다)
예: 문자열
ASCII 코드 : C=67, L=76, R=82, S=83
128진수로 표현하는 문자열 CLRS는(임의의 문자열을 자연수로 해석하기 위해)
(67*128^3) + (76*128^2) + (82*128^1) + (83*128^0) = 141,764,947
해시 함수의 간단한 예
h(k) = k % m
즉, key를 하나의 자연수로 해석한 후 테이블의 크기 m으로 나눈 나머지를 데이터가 저장될 주소로 사용 한다.
항상 0 ~ m-1 사이의 정수가 됨
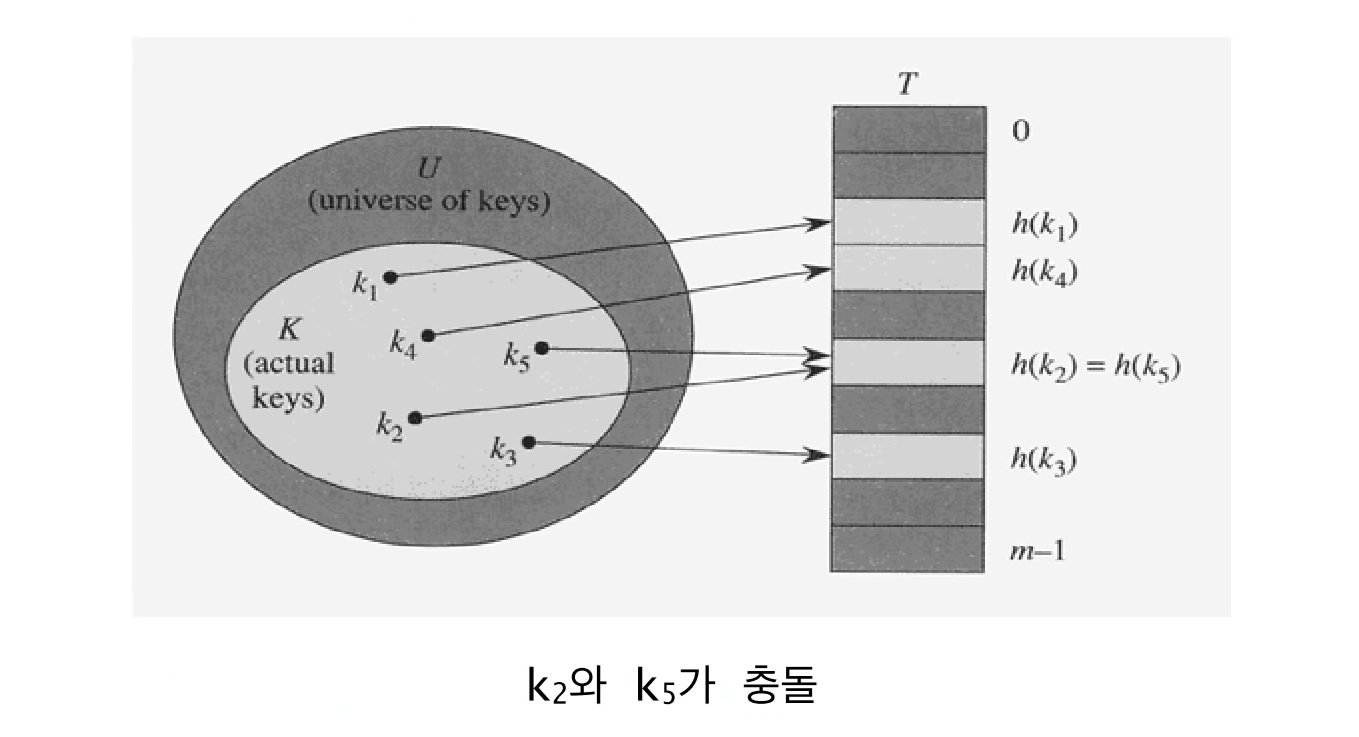
충돌(collision)
두 개 이상의 키가 동일한 위치로 해싱되는 경우
즉, 서로 다른 두 키 k1과 k2에 대해서 h(k1) = h(k2)인 상황
일반적으로|U| >> m 이므로 항상 발생 가능 (즉, 일반적으로 해시함수는 단사함수가 아님)
만약 |K| > m 이라면 당연히 발생, 여기서 K는 실제로 저장된 키들의 집합
임의의 정수를 저장하기 위한 배열의 크기를 무한정 키울수는 없다.
충돌이 발생할 경우 대처 방법이 필요하다
대표적인 두 가지 충돌 해결방법
chainging
open addressing
Chaining에 의한 충돌 해결
동일한 장소로 해싱된 모든 키들을 하나의 연결리스트(Linked List)로 저장

키의 삽입(Insertion)
키 k를 리스트 T[h(k)]의 맨 앞에 삽입 : 시간복잡도는 O(1)
중복된 키가 들어올 수 있고 중복 저장이 허용되지 않는다면 삽입시 리스트를 검색해야 한다. 따라서 이런경우 삽입의 시간복잡도는 리스트의 길이에 비례한다.
키의 검색(Search)
리스트 T[h(k)]에서 순차검색
시간복잡도는 키가 저장된 리스트의 길이에 비례한다.
키의 삭제(Deletion)
리스트 T[h(k)]로 부터 키를 검색 후 삭제
일단 키를 검색해서 찾은 후에는 O(1)시간에 삭제가 가능하다.
최악의 경우는 모든 키가 하느의 슬롯으로 해싱되는 경우이다.
길이가 n인 하나의 연결리스트가 만들어지고
따라서 최악의 경우 탐색시간은 O(n) + 해시함수 계산시간이 된다.
평균 시간복잡도는 키들이 여러 슬롯에 얼마나 잘 분배되느냐에 의해서 결정 된다.
SUHA (Simple Uniform Hashing Assumption)
각각의 키가 모든 슬롯들에 균등한 확률로(eually likely) 독립적으로(independently) 해싱된다는 가정
성능분석을 위해서 주로 하는 가정임
hash함수는 deterministic(결정적 함수이므로)하므로 현실에서는 불가능하다.
특정한 키 값의 해시함수 값은 정해져 있다.
위의 가정이 성립한다면(키가 해시테이블에 저장될 확률이 동일 하다면) Load factor를 정의할 수 있다.
Load factor a = n/m
n : 테이블에 저정될 키의 개수
m : 해시테이블의 크기, 즉 연결리스트의 개수
각 슬롯에 저장된 키의 평균 개수
연결리스트 T[j]의 길이를 n-j이라고 하면 E[n-j] = a
만약 n=O(m)이면 평균검색시간은 O(1)
강의 맨 처음에 "적절한 가정"하에 평균 탐색, 삽입, 삭제시간 O(1)이라는 이야기를 했었는데, '적절한 가정'이 성능분석을 위해 주로 하는 현실에서는 불가능한 가정이므로 가설이라고 이야기 할 수 있다.
Open Addressing에 의한 충돌 해결
모든 키를 해시 테이블 자체에 저장
테이블의 각 칸(slot)에는 1개의 키만 저장
충돌 해결 기법
Linear probing
Quadratic probing
Double hashing
Linear Probing
h(k), h(k) + 1, h(k) + 2, … 순서로 검사하여 처음으로 빈 슬롯에 저장 테이블의 끝에 도달하면 다시 처음으로 circular하게 돌아감
search하는 경우에는 순차적으로 찾을때 까지 검색하다가 빈 슬롯이 나오면 종료

다른 방법들
Linear probing의 단점
primary cluster : 키에 의해서 채워진 연속된 슬롯들을 의미
이런 cluster가 생성되면 이 cluster는 점점 더 커지는 경향이 생김
검색시간이 클러스터의 길이에 비례하게 되므로 바람직하지 않다.
Quadratic probing
충돌 발생시 h(k), h(k) + 1^2, h(k) + 2^2, h(k) + 3^2, … 순서로 시도
Double hashing
서로 다른 두 해시 함수 h1과 h2를 이용하여
h(k, i) = (h1(k) + i*h2(k)) mod m
Quadratic Probing
충돌 발생시 h(k), h(k) + 1^2, h(k) + 2^2, h(k) + 3^2, … 순서로 시도
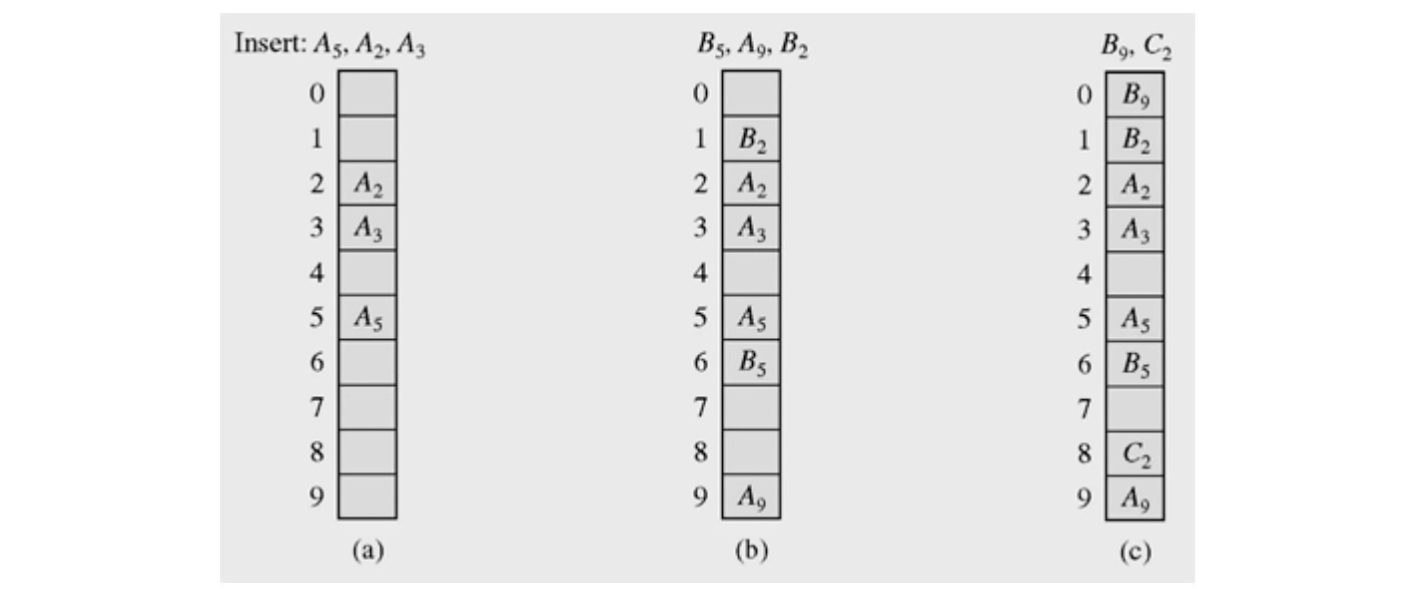
Double Hashing
서로 다른 두 해시 함수 h1과 h2를 이용한다.
키 값에 따라서 해시 값이 달라진다.

Open Addressing - 키의 삭제
단순히 키를 삭제할 경우 문제가 발생한다.
가령 A2, B2, C2기 순서대로 모두 동일한 해시함수값을 가져서 linear probing으로 충돌을 해결했을 때,
B2를 삭제한 후 C2를 검색하는 경우가 이에 해당한다.
Linear Probing을 했을 경우 빈 슬롯에 도달하면 검색이 종료되기 때문에 검색에 문제가 생기게 된다.
이 문제를 해결하기 위해서 삭제된 슬롯에 예를 들면 DEL이라는 표시를 해둘 수도 있지만,
Dynamic Set을 구현한 해시 테이블의 특성상 삽입, 삭제가 빈번하게 일어나므로 결국 거의 모든 슬롯이 DEL표시로 채워질 수 있다.
또한, 곳곳에 DEL 표시가 되어있으면 결국 배열과 같이 모든 슬롯을 검색하게 되므로 Hashing의 장점을 잃게 된다.
가장 적절한 해결책은 삭제될 슬롯에 있는 값과 같은 해시값을 가지는 클러스터의 마지막 슬롯을 삭제될 슬롯으로 가져와서 클러스터의 손상을 막는 방법이다.
'ICT Eng > Algorithm' 카테고리의 다른 글
| [Algorithm] 7-1. Graph 01 - 개념과 표현 (0) | 2018.04.27 |
|---|---|
| [Algorithm] 6-2. Hash 함수, Hashing in Java (0) | 2018.04.17 |
| [Algorithm] 5-3. Red Black Tree 03 - DELETE, FIXUP 연산 (3) | 2018.04.07 |
| [Algorithm] 5-2. Red Black Tree 02 - INSERT, FIXUP 연산 (0) | 2018.03.29 |
| [Algorithm] 5-1. Red Black Tree 01 - 개요 (0) | 2018.03.29 |
- Total
- Today
- Yesterday
- Spring Boot
- Spring
- vuex
- Raspberry Pi
- 인프런
- 스프링부트
- JPA
- 정렬
- 알고리즘
- IT융합인력양성사업단
- 한밭이글스
- 젠킨스
- github
- 레드블랙트리
- AWS
- 라즈베리파이
- Recursion
- 한밭대학교
- Vue.js
- RBT
- Wisoft
- Algorithm
- 자바
- Java
- 무선통신소프트웨어연구실
- ORM
- springboot
- 시간복잡도
- vuejs
- 순환
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 |
