티스토리 뷰
[Algorithm] 7-2. Graph 02 - BFS(Breadth-First Search, 너비우선탐색)
nroo 2018. 4. 27. 03:27영리한 프로그래밍을 위한 알고리즘 강좌 '(링크)와 '쉽게 배우는 알고리즘 관계 중심의 사고법 - 문병로' 참조
7-2. Graph 02 - BFS(Breadth-First Search, 너비우선탐색)
그래프 순회
순회(traversal)
그래프의 모든 노드들을 방문하는 일
대표적 두 가지 방법
BFS (Breadth-First Search, 너비우선순회)
DFS (Depth-First Search, 깊이우선순회)
너비우선탐색(BFS)
BFS 알고리즘은 다음 순서로 노드들을 방문
L0 = {s}, 여기서 s는 출발 노드
L1 = L0의 모든 이웃 노드들
L2 = L1의 이웃들 중 L0에 속하지 않는 노드들
...
Li = Li-1의 이웃들 중 Li-2에 속하지 않는 노드들
한마디로 그래프에서 노드들을 동심원의 형태로 순회하는 방법

큐를 이용한 너비우선탐색
출발노드를 check하고 시작한다.
큐에 스타트 노드(1번노드)를 삽입한다.
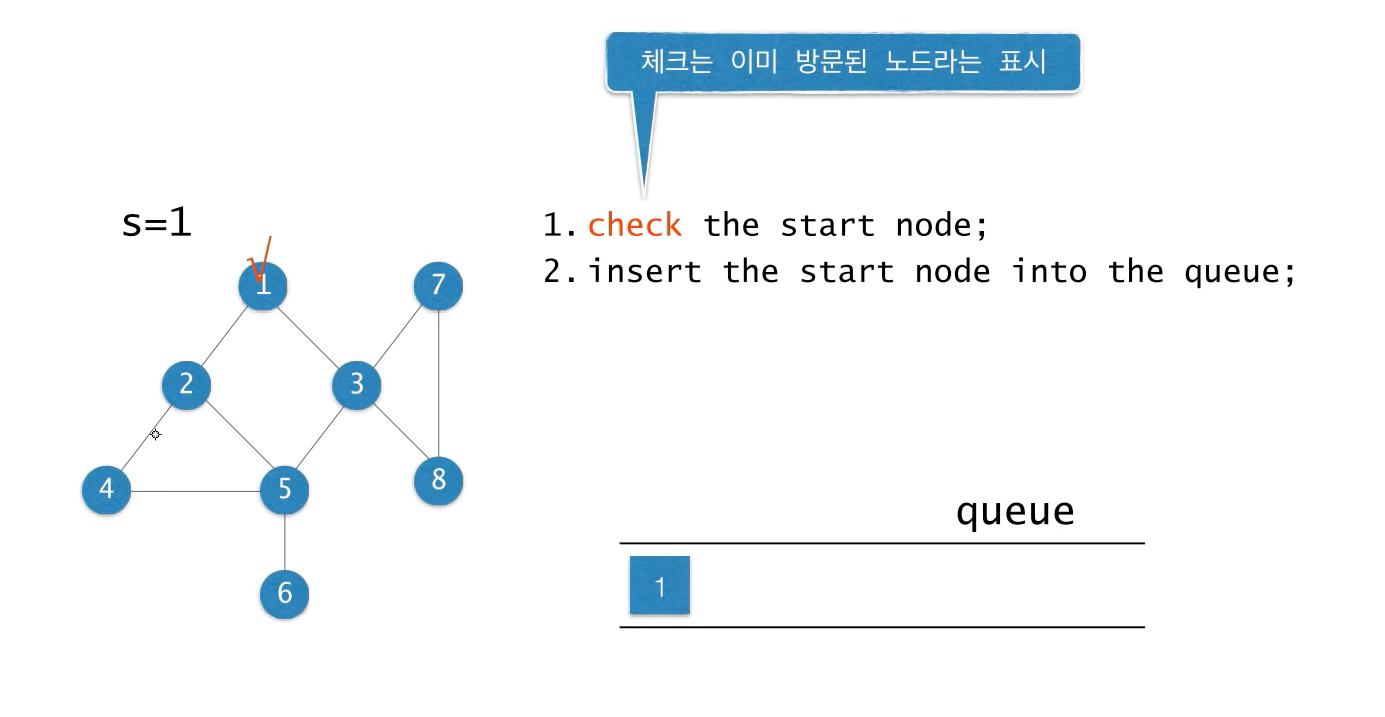
whil문을 돌면서 큐가 비어있을 때까지 반복한다.
큐에서 노드(v)를 하나 꺼내고
꺼낸 노드의 인접노드 중, 아직 방문되지 않은(unchecked) 노드들(w)을 체크하고 큐에 넣는다.
이 때, 큐에 넣는 순서는 중요하지 않다.
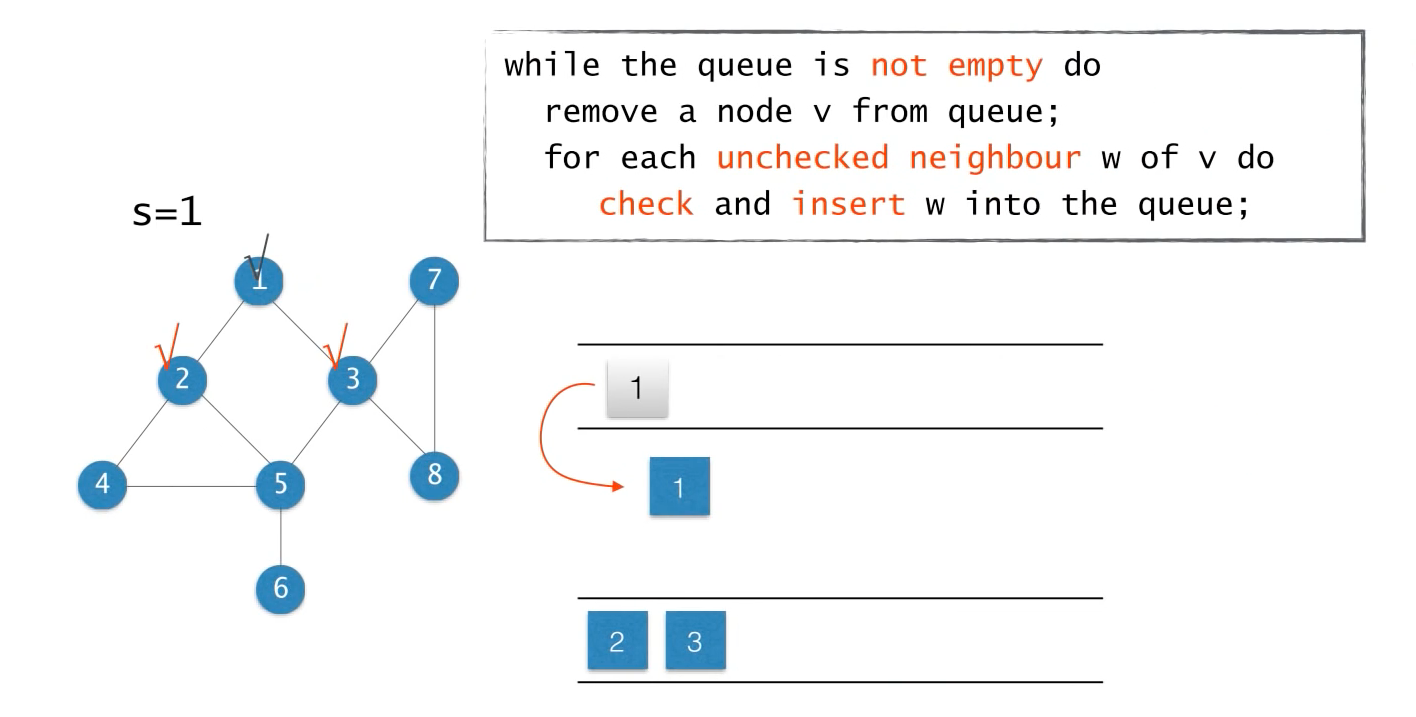
다시 큐에서 노드를 하나 꺼내고(2번 노드)
2번 노드의 체크되지 않은 인접 노드들(4, 5번 노드)을 체크상태로 변경하고 큐에 넣는다.
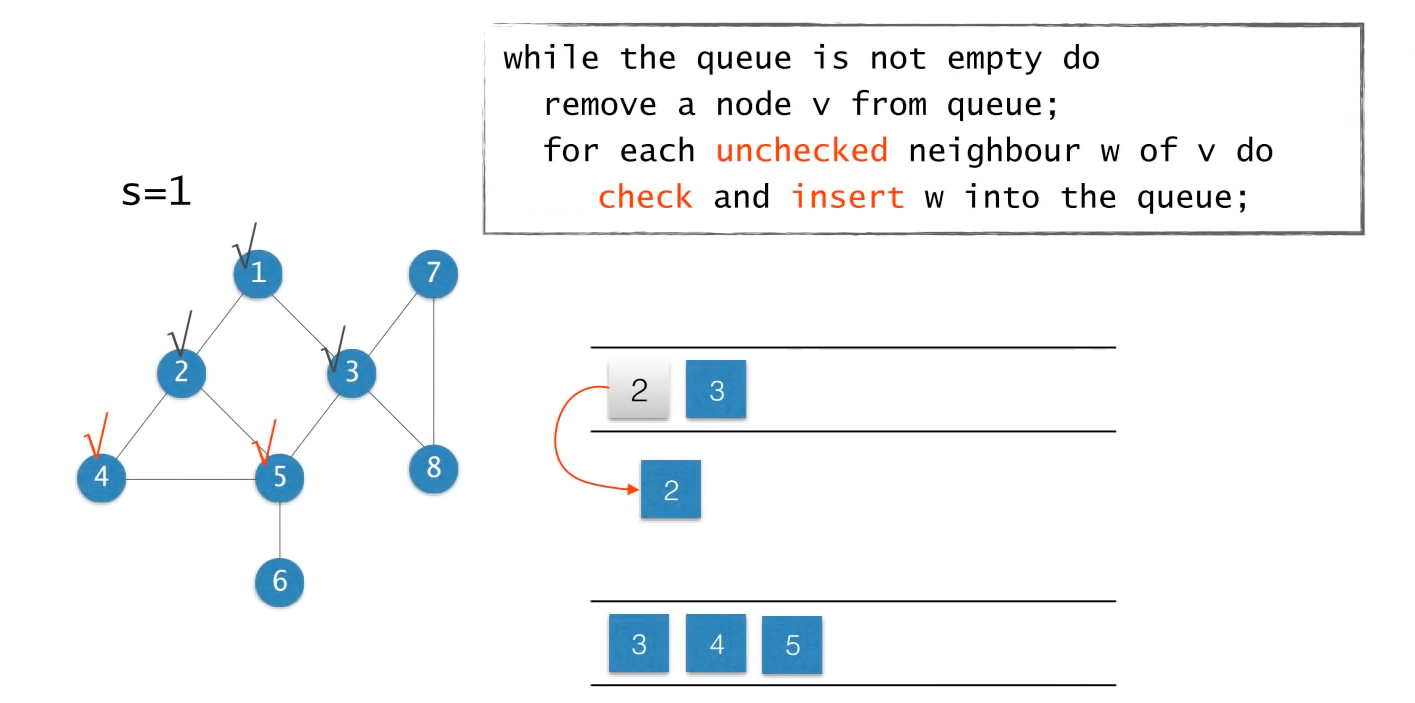
이런 방법으로 큐가 비어있는 상태가 될때까지 반복한다.
최종적으로 노드를 방문한 순서는 1, 2, 3, 4, 5, 7, 8, 6 이 된다. 하지만, 이 방문 순서는 유일하지 않다. 큐에 인접노드를 삽입하는 순서에 따라 달라지기 때문이다.
BFS pesudo code
그래프 G, 출발 노드 S
00 BFS(G, s)
01 Q <- null;
02 Enqueue(Q, s);
03 while Q != null do
04 u <- Dequeue(Q);
05 for each v adjacent to u do
06 if v is unvisited then
07 mark v as visited;
08 Enqueue(Q, v);BFS와 최단경로
BFS는 단순히 그래프의 모든 노드를 방문하는 것 이상의 추가적인 중요한 일을 할 수 있다. 최단 경로를 구하는 일이다.
s에서 Li에 속한 노드까지 최댄 경로의 길이는 i이다.
여기서 경로의 길이는 경로에 속한 엣지의 수를 의미한다.
BFS를 하면서 각 노드에 대해서 최단 경로의 길이를 구할 수 있다.
입력
방향 혹은 무방향 그래프 G = (V, E), 그리고 출발노드 s
출력
모든 노드 v에 대해서
d[v] = s로 부터 v까지의 최단 경로의 길이(엣지의 개수)
π[V] = s로 부터 v까지의 최단경로상에서 v의 직전 노드(predecessor)
Pseudo code
02 - 04 : 모든 노드 u에 대해서 d[], π[]를 초기화
05 - 06 : 스타트 노드의 d[], π[]를 설정
11 : d[v] 가 -1인가를 체크하여 unvisited 체크를 구현
12 - 13 : unvisited 노드에 대하여 d[v], π[v]를 저장
최단경로 길이 d[v]는 u까지의 최단경로길이 d[u]를 지나오는 것이므로 d[u] + 1이 될 것이고,
v노드의 최단경로상에서 v의 직전노드는 u가 된다.
14 : unchecked 노드만 큐에 들어갈 수 있으므로 어떤 노드도 큐에 두번 들어가지는 않는다.
00 BFS(G, s)
01 Q <- null;
02 for each node u do
03 d[u] <- -1;
04 π[u] <- null;
05 d[s] <- 0; //distance from s to s is 0
06 π[s] <- null; //no predecessor of s
07 Enqueue(Q, s);
08 while Q != null do
09 u <- Dequeue(Q);
10 for each v adjacent to u do
11 if (d[v] == -1) then
12 d[v] <- d[u] + 1; //distance to v
13 π[v] <- u; //u is the predecessor of v
14 Enqueue(Q, v);시간복잡도
02라인 for 의해 기본적으로 O(n)이다.
실제로는 08라인의 while문이 알고리즘의 시간복잡도를 결정한다.
기본적으로 while문이 한번 돌 때마다 큐에서 노드 하나씩 꺼내므로 while문은 최대 n번 돈다.
10라인의 for문은 u의 degree() 만큼 돈다. 리스트를 인접 행렬로 구현하느냐, 인접리스트로 구현하느냐에 따라 for문의 시간복잡도가 달라진다.
degree(v)는 어떤 한 노드 v에 실제로 인접한 노드의 수
그래프를 인접 행렬로 구현할 경우 degree(v)를 찾으려면 O(n)이 든다. 따라서 인접행렬로 구현했을 떄의 while문의 시간복잡도는 O(n^2)이 된다.
인접 리스트로 구현할 경우 전체 그래프에서 보면, for 문은 결국 모든 노드들의 degree() 만큼 돌 것이다. 인접리스트에서 그것은 2m이다.(무방향 그래프에서 총 엣지의 수) 시간복잡도는 O(m). 따라서, while문의 시간복잡도는 O(n + m)이 된다.
결과적으로 인접 리스트의 최악의경우 m이 n이 되므로 최악의 경우가 아닌 이상 인접 리스트로 구현하는 것이 좀 더 효율적이다.
BFS로 구현한 d[]와 π[] 예시
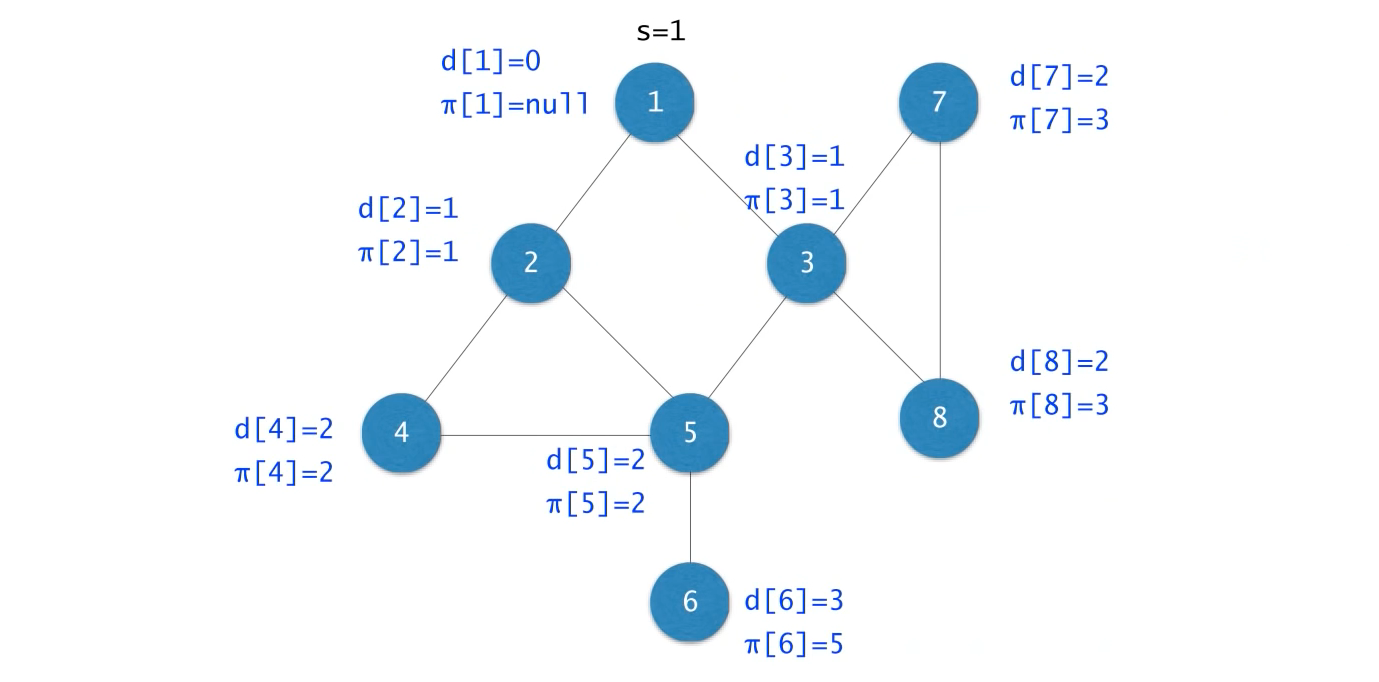
BFS 트리
각 노드 v와 π[v]를 연결하는 엣지들로 구성되는 트리
BFS 트리에서 s에서 v까지의 경로는 s에서 v까지 가는 최단 경로
어떤 엣지도 동심원의 2개의 layer(L0에서 L2로 가지 않는다)를 건너가지 않는다.(동일 레이어의 노드를 연결하거나, 혹은 1개의 layer를 건너간다.)

너비우선탐색: 최단 경로 출력하기
출발점 s에서 노드 v까지의 경로 출력하기
resursion으로 해결한다.
s에서 v까지 가는 최단 경로는 먼저 s에서 π[v]까지 가는 경로를 출력하고, v를 추가로 출력하면 된다.
00 PRINT-PATH(G, s, v)
01 if v = s then
02 print s;
03 else if π[v] = null then // 실제로 s에서 v까지 가는 경로가 없을 경우(최단경로도 없음)
04 print "no path from s to v exists";
05 else
06 PRINT-PATH(G, s, π[v]);
07 print v;너비우선탐색(BFS) 정리
그래프가 connected 라면 모든 노드를 방문하게 된다. 하지만, 그래프가 disconnected 이거나 혹은 방향 그래프라면 BFS에 의해서 모든 노드가 방문되지 않을 수도 있다.
disconnected 그래프의 모든 노드를 방문하려면 BFS를 반복하여 모든 노드 방문
전체 노드중 unvisited 노드가 없을 때까지 BFS를 반복한다.
BFS-ALL(G)
while there exists unvisited node v
BFS(G, V)'ICT Eng > Algorithm' 카테고리의 다른 글
| [Algorithm] 7-3. Graph 03 - DFS(Depth-First Search, 깊이우선탐색) (0) | 2018.04.29 |
|---|---|
| [Algorithm] 7-1. Graph 01 - 개념과 표현 (0) | 2018.04.27 |
| [Algorithm] 6-2. Hash 함수, Hashing in Java (0) | 2018.04.17 |
| [Algorithm] 6-1. Hashing 개요 - Chaining, Open Addressing, SUHA (0) | 2018.04.17 |
| [Algorithm] 5-3. Red Black Tree 03 - DELETE, FIXUP 연산 (3) | 2018.04.07 |
- Total
- Today
- Yesterday
- 라즈베리파이
- Spring
- vuejs
- AWS
- Spring Boot
- RBT
- 한밭이글스
- 레드블랙트리
- 정렬
- 무선통신소프트웨어연구실
- 알고리즘
- Algorithm
- springboot
- 인프런
- 자바
- 젠킨스
- IT융합인력양성사업단
- github
- Recursion
- Wisoft
- 한밭대학교
- 스프링부트
- vuex
- Vue.js
- JPA
- Raspberry Pi
- 순환
- 시간복잡도
- ORM
- Java
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
