티스토리 뷰
부경대 IT융합응용공학과 권오흠 교수님의 영리한 프로그래밍을 위한 알고리즘 강좌와 '쉽게 배우는 알고리즘: 관계중심의 사고법 - 문병로'등을 통한 알고리즘 학습 강좌 링크
3-3. 빠른정렬(Quick Sort)
분할정복법
분할
배열을 다음과 같은 조건이 만족되도록 두 부분으로 나눈다.
기준값 : pivot
elements in lower parts <= elements in upper parts
pivot을 기준으로 작은값들, 큰값들로 나눈다.
정복
각 부분을 순환적으로 정렬한다.
합볍
각 부분을 순환적으로 정렬했다면, 그것으로 이미 전체가 정렬 되어 있는 상태가 된다.
nothing to do
Quicksort
정렬할 배열이 주어진다. 마지막 수를 기준(pivot)으로 삼는다.
| 31 | 8 | 48 | 73 | 11 | 3 | 20 | 29 | 65 | 15 |
|---|
기준(15)보다 작은 수는 기준의 왼쪽에 나머지는 기준의 오른쪽에 오도록 재배치(분할)한다.
| 8 | 11 | 3 | 15 | 31 | 48 | 20 | 29 | 65 | 73 |
|---|
기준의 왼쪽과 오른쪽을 각각 순환적으로 정렬한다(정렬 완료)
| 3 | 8 | 11 | 15 | 20 | 29 | 31 | 48 | 65 | 73 |
|---|
Algorithm
마찬가지로 quicksort도 recursion이므로 매개변수를 명시화 시킨다.
quickSort(A[], p, r) {
base case;// p>=r일 때, 정렬할 데이터가 0개 또는 1개이므로 할 일 없음.
if (p < r) then {
q = partition(A, p, r); //pivot의 위치
quickSort(A, p, q-1);
quickSort(A, q+1, r);
}
}
partition(A[], p, r) {
배열 A[p...r]의 원소들을 A[r]을 기준으로 양쪽으로 재배치하고 A[r]이 자리한 위치를 return 한다;
}Partition

순환적으로 pivot을 기준으로 정렬을 진행하다가, 마지막에 pivot과 큰 값들 중 첫번째 값을 바꾼다.
아래와 같은 방법으로 pivot보다 작은 값, 큰값들로 나눈다.
새로운 값(A[j])를 봤더니, pivot보다 크다면 j를 1증가시켜서 큰 값들의 범위를 하나 늘린다.
반대로, pivot보다 작다면, i를 하나 증가시키고 새로운값 A[j]과 교환하면, 여전히 맨 앞 부터 i까지는 pivot보다 작은 값들이 위치하게 된다.
다음으로 j를 1증가시키면 pivot보다 큰 값들의 범위도 유지가 된다.
if A[j] >= x
j <- j+1;
else
i <- i+1;
exchange A[i] and A[j];
j <- j+1;예를 들면, 아래와 같은 흐름으로 i와 j가 움직이게 된다.
시작인덱스 p, 끝인덱스 r
맨 처음에 pivot보다 작다고 판정된 값은 아무것도 없으므로, i는 p-1로 시작한다. j는 p로 시작한다.
pivot인 15보다 31이 크므로 j를 증가시킨다.
다음 값인 8은 15보다 작으므로 i를 1증가시키고 i와 j를 교환한 뒤, j를 1증가 시킨다.
그 다음 값은 48은 15보다 크므로 j를 1증가시킨다.
...


마지막으로 j와 r이 같아지면, pivot값과 pivot보다 큰 값들중 첫번째 값인 73을 교환하고,
결과적으로 pivot보다 작은 값들의 집합, pivot, pivot보다 큰 값들의 집합으로 partition이 형성된다. 그리고 pivot의 index를 리턴해주면 된다.
이것을 psedocode로 표현하면 다음과 같다.
시작인덱스 = p
마지막인덱스 = r
pivot = x
i = p-1
j = p
parition에서는 n-1번의 비교연산을 가지므로, O(n)의 시간이 걸린다.
partition(A, p, r) {
x <- A[r];
i <- p-1;
for j <- p to r-1
if A[j] <= x then
i <- i+1;
exchange A[i+1] and A[r];
exchange A[i+1] and A[r];
return i+1;
}최악의 경우
항상 한 쪽은 0개, 다른 쪽은 n-1개로 분할되는 경우
n(n-1)/2가 되므로, 최악의 경우 매우 비효율적인 알고리즘이 된다.

이미 정렬된 입력 데이터 (마지막 원소를 피봇으로 선택하는 경우)를 Quick Sort하는 경우가 위의 경우이다. 항상 한 쪽은 0개, 다른쪽은 n-1개로 분할된다.
이미 정렬된 배열에서 마지막 원소를 피봇으로 봤을때, 나머지 원소들은 다 피봇보다 작은 값이 된다.
그 다음 1 ~ n-1 번째 까지의 원소에서도 마지막 원소인 피봇보다 나머지 원소들이 다 작은 값이다.
최선의 경우
항상 절반으로 분할 되는 경우
이 경우에는 merge sort와 같은 시간복잡도를 갖는다.
T(n) = 2T(n/2) + Θ(n)
= Θ(nlogn)
극단적인 경우가 아니라면
실제 사용을 해보면 다른 sorting알고리즘 보다 빠르기 떄문에, Quick Sort라는 이름이 붙여졌다. 그러나 최악의 경우 Θ(n²)의 시간복잡도를 가지므로, mergesort의 O(nlogn)보다 훨씬 나쁘다. 사실 최악의 경우와 최선의 경우가 발생할 확률은 드물다.
아래의 그림을 통해 quick sort가 빠르다는 것에 대한 설명을 보충 한다.
항상 한쪽이 적어도 1/9 이상이 되도록 분할된다면? (가정이다.)
항상 1:9로 분할 되면 왼쪽 트리보다 오른쪽 트리가 훨씬더 길게 그려질 것이다.
가장 오른쪽의 트리를 보면 1이 될 때까지 트리가 그려지므로
(9/10)<sup>k</sup> * n = 1 을 계산하면 k = log<sub>10/9</sub>n이 된다.
따라서, 층의 최대 갯수는 Θ(logn)이다.
추가적으로, 한 레벨씩 아래로 내려올때매다 n번의 비교연산을 하게 되므로, 결국 quick sort의 시간복잡도는 Θ(nlogn)이 된다.
이 증명으로 Quick Sort 최악의 경우 시간복잡도가 Θ(n²)임에도 불구하고, 실제로는 상당히 빠른 것에 대한 직관적인 설명이 될 수 있다. 분할이 극단적으로만 일어나지 않는다면 충분히 빠른 정렬알고리즘이다.

평균시간복잡도
"평균" 혹은 "기대값"이란?
어떤 사건이 일어날 확률 * 그 사건이 일어났을 때의 시간
quick sort 알고리즘에 n개의 데이터가 들어왔을때, 평균시간복잡도를 A(n)이라고 했을때,
크기가 n인 모든 가능한 입력 I에 대해서 p(I)T(I)이다.
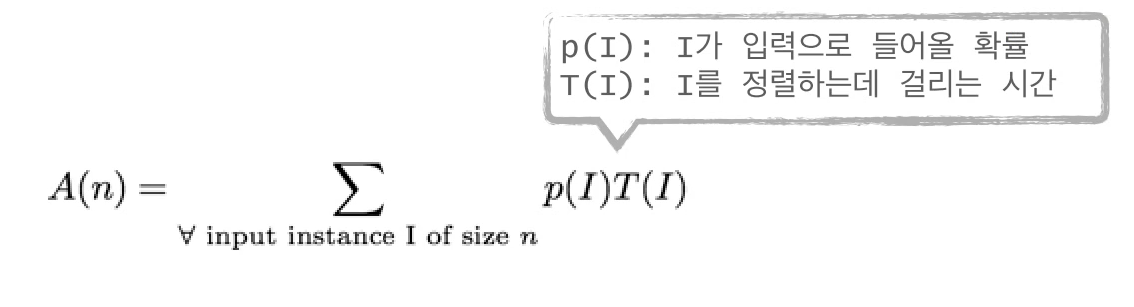
그러나, p(I)를 모른다.
p(I)에 관한 적절한 가정을 한 후 분석한다.
예: 모든 입력 인스턴스가 동일한 확률을 가진다면
1 ~ n개의 정수가 입력으로 들어온다면, 1 ~ n개의 정수를 섞어서 만들 수 있는 순열의 수는 n!개이다. 따라서, n!개의 순열이 각각 입력으로 들어올 경우의 수는 동일하다.
p(I) = 1/n!
1 ~ n 중 맨 마지막 원소를 pivot으로 봤을 때, 이 pivot이 가장 작은 값일 경우(rank of pivot이 1인 경우)부터 가장 큰 값일 경우(rank of pivot이 n인 경우) 총 n개의 경우의 수가 있다.
그러면, 그런 경우가 발생할 probability는 1/n으로 모두 같다.
만약 rank of pivot이 3이라서, result of partition이 2:n-3으로 나누어 졌을 때,
추가적으로 드는 running time은 A(2) + A(n-3)만큼 이다.
결국 평균 시간 복잡도는 n개의 경우의 수에 대해 running time 곱하기 확률(1/n)을 해주면 된다.
아래 그림에서 시그마 앞의 상수는 2/n 이다.(n/2로 표기오류된 부분) A(0) ~ A(n-1)까지 총 두번.
추가적으로 분할을 하는데 걸리는 시간은 항상 동일하게 Θ(n)이다.
아래의 순환식을 풀어보면 quick sort의 평균 시간복잡도는 Θ(nlogn)이 된다.
따라서, 결론적으로 평균시간복잡도까지 구해본 결과, 극단적인 최악의 경우가 아니라면, 실제로 빠른 정렬 알고리즘이다라는 것에 대한 증명을 할 수 있다.

Pivot의 선택
첫번째 값이나 마지막 값을 피봇으로 선택
이미 정렬된 데이터 혹은 거꾸로 정렬된 데이터가 최악의 경우가 된다.
현실의 데이터는 랜덤하지 않으므로 (거꾸로) 정렬된 데이터가 입력으로 들어올 가능성은 매우 높다.(사전에 다른 소프트웨어에 의해 정렬된 데이터가 넘어오는 경우)
따라서 좋은 방법이라고 할 수 없다.
"Median of Three"
첫번째 값과 마지막 값, 그리고 가운데 값 중에서 중간값(median)을 피봇으로 선택
최악의 경우 시간 복잡도가 달라지지는 않음
Randomized Quicksort
피봇을 랜덤하게 선택
no worst case instance, but worst case execution
다른 방법의 경우, 어떤 입력이 최악의 경우이다 라는 것이 정해지지만, 피봇을 랜덤하게 선택하면 어떤 데이터가 들어오더라도 랜덤값에 의해 결정 되므로. 최악의 실행이 존재한다.
평균 시간복잡도 O(NlogN)
'ICT Eng > Algorithm' 카테고리의 다른 글
| [Algorithm] 3-5. 우선순위 큐(priority queue) (0) | 2018.01.26 |
|---|---|
| [Algorithm] 3-4. Heap Sort(힙정렬) (2) | 2018.01.24 |
| [Algorithm] 3-2. Merge Sort(합병정렬) (0) | 2018.01.19 |
| [Algorithm] 3-1. 기본 정렬 알고리즘(selection, bubble, insertion sort) with JAVA (1) | 2018.01.17 |
| [Algorithm] 2-7. Recursion 응용 4 - 멱집합, PowerSet (0) | 2018.01.14 |
- Total
- Today
- Yesterday
- 순환
- RBT
- 젠킨스
- vuex
- Wisoft
- 자바
- ORM
- github
- Spring Boot
- springboot
- 알고리즘
- 시간복잡도
- Algorithm
- Raspberry Pi
- JPA
- 인프런
- IT융합인력양성사업단
- 레드블랙트리
- 정렬
- Java
- 한밭이글스
- AWS
- vuejs
- 한밭대학교
- 무선통신소프트웨어연구실
- Spring
- 스프링부트
- 라즈베리파이
- Recursion
- Vue.js
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
