티스토리 뷰
부경대 IT융합응용공학과 권오흠 교수님의 영리한 프로그래밍을 위한 알고리즘 강좌와 '쉽게 배우는 알고리즘: 관계중심의 사고법 - 문병로'등을 통한 알고리즘 학습 강좌 링크
2-7. Recursion의 응용 4 - 멱집합
멱집합 - Powerset
어떤 집합의 모든 부분집합을 멱집합이라고 부른다.
임의의 집합 data = {a, b, c, d}의 모든 부분집합은
2ⁿ = 16개 이다.
Recursion을 이용하여 모든 부분집합을 나열
{a, b, c, d, e, f}의 모든 부분집합을 나열하려면
먼저 a를 포함하지 않는 부분집합과
a를 포함하는 부분집합으로 나눌 수 있다.
따라서, 아래와 같이 표현할 수 있다.
a를 포함하지 않는 부분집합
a를 제외한 {b, c, d, e, f}의 모든 부분집합들을 나열하고
a를 포함하는 부분집합
{b, c, d, e, f}의 모든 부분집합에 {a}를 추가한 집합들을 나열한다.
위의 두가지를 합치면 경우의 수가 2ⁿ개가 되는 것이다.
그렇다면, {b, c, d, e, f}의 모든 부분집합에 {a}를 추가한 집합들을 나열하려면
다시 한번 b를 포함하지 않는 부분집합과
b를 포함하는 부분집합으로 나누어 생각한다.
따라서,
b를 포함하지 않는 부분집합
{c, d, e, f}의 모든 부분집합들에 {a}를 추가한 집합들을 나열하고
b를 포함하는 부분집합
{c, d, e, f}의 모든 부분집합에 {a, b}를 추가한 집합들을 나열한다.
다시, {c, d, e, f}의 모든 부분집합에 {a}를 추가한 집합들을 나열하려면
{d, e, f}의 모든 부분집합들에 {a}를 추가한 집합들을 나열하고
{d, e, f}의 모든 부분집합에 {a, c}를 추가한 집합들을 나열한다.
Recursion으로 표현
S의 멱집합을 출력하라
아래와 같이 S에서 t를 뺀 집합의 모든 부분집합을 구하고 return을 하면,
모든 부분집합을 저장해야하기 때문에, 모든 부분집합을 출력하는 문제를 해결하는데에는 적합하지 않을 수 있다.
powerSet(S)
if S is an empty set
print nothing;
else
let t be the first element of s;
find all subsets of S-{t} by calling powerSet(S-{t});
return all of them;따라서, 아래와 같이 변경을 한다.
else문에서 보면 S에서 t를 뺀 집합의 모든 부분집합을 구하고 print해주는 부분이 있다.
하지만, 이렇게 변경을 해도 모든 부분집합에 t를 추가한 집합들을 나타내는 subsets with adding t를 해결할 수 없다. 코드에서 모든 부분집합을 저장하지 않았기 때문에.
powerSet(S)
if S is an empty set
print nothing;
else
let t be the first element of s;
find all subsets of S-{t} by calling powerSet(S-{t});
print the subsets;
print the subsets with adding t;resursion의 설계 자체를 수정해야 할 필요가 있다.
위의 recursion 구현에서 결과적으로 모든 부분집합에 t를 추가한 집합들을 나타내는 작업을 수행하는데서 문제가 있었다. 아래의 단계이다.
{b, c, d, e, f}의 모든 부분집합에 {a}를 추가한 집합들을 나열한다.
b를 포함하지 않는 부분집합
{c, d, e, f}의 모든 부분집합들에 {a}를 추가한 집합들을 나열하고
b를 포함하는 부분집합
{c, d, e, f}의 모든 부분집합에 {a, b}를 추가한 집합들을 나열한다.
위의 단계중에 {c, d, e, f}의 모든 부분집합에 {a, b}를 추가한 집합들을 나열하려면,
어떤 집합의 모든 부분집합을 구해서, 그 결과에 또 다른 집합을 추가해서 출력하는 일을 할 수 있도록 설계가 바뀌어야 한다.
Mission : S의 멱집합을 구한 후 각각에 집합 P를 합집합하여 출력하라
S : {c, d, e, f} - k번째 부터 마지막 원소까지 연속된 원소들이다.
P : {a, b} - 처음부터 k-1번째 원소들 중 일부이다.
recursion 함수가 두 개의 집합을 매개변수로 받도록 설계해야 한다는 의미이다. 두 번째 집합의 모든 부분집합들에 첫번째 집합을 합집합하여 출력한다.
맨 처음 초기 호출은 powerSet(null, S)으로 하면 된다. S의 멱집합을 구하기 위한 호출이다.
powerSet(P, S)
if S is an empty set
print P;
else
let t be the first element of S;
powerSet(P, S-{t});
powerSet(P 합집합 {t}, S-{t});S와 P를
S : k번째 부터 마지막 원소까지 연속된 원소들이다.
P : 처음부터 k-1번째 원소들 중 일부이다.
아래와 같이 S와 P를 k라는 인덱스와 P라는 boolean 배열을 이용해서 나타낸다.

Powerset Java 구현
Mission : data[k], … , data[n-1]의 멱집합을 구한 후 각각에 include[i]=true, i=0,…,k-1, 인 원소를 추가하여 출력하라.
처음 함수 호출은 powerSet(0)으로 호출한다. 즉, P는 공집합 S는 전체집합.
data[] 배열 중에서 인덱스 k부터 마지막까지 집합 S이고,
data[] 배열 중에서 인덱스 0부터 k-1까지의 집합중 true인 값을 가지고 있는 것 들이 집합 P이다. 그리고 이것은 include로 표현한다.
Base case는 집합 S가 공집합일 경우이다. 그 경우에는 그냥 P를 출력하면 된다. data중에 include에서 유지하고 있는 값이 true인 요소들.
일반적인 경우에는
data[k]를 포함하지 않는 경우
data[k]가 'a'라고 할 때, include[k]를 false로 놓고 powerSet의 매개변수를 'b'부터 끝원소까지의 집합으로 재귀호출한다.
include[k] = false;
powerSet(k + 1);data[k]를 포함하는 경우
data[k]가 'a'라고 할 때, include[k]를 true로 놓고 powerSet의 매개변수를 'b'부터 끝원소까지의 집합으로 재귀호출한다.
include[k] = true;
powerSet(k + 1);
private static char data[] = {'a','b','c','d','e','f'};
private static int n = data.length;
private static boolean[] include = new boolean[n];
public static void powerSet(int k) {
if (k == n) {
for (int i = 0; i < n; i++)
if (include[i])
System.out.print(data[i] + " ");
System.out.println();
return;
}
include[k] = false;
powerSet(k + 1);
include[k] = true;
powerSet(k + 1);
}상태공간트리 (state space tree)
원소가 {a, b, c}일 때, 구할 수 있는 모든 부분집합을 나타내는 트리이다.
include와 exclude가 반대로 표기되어있다.
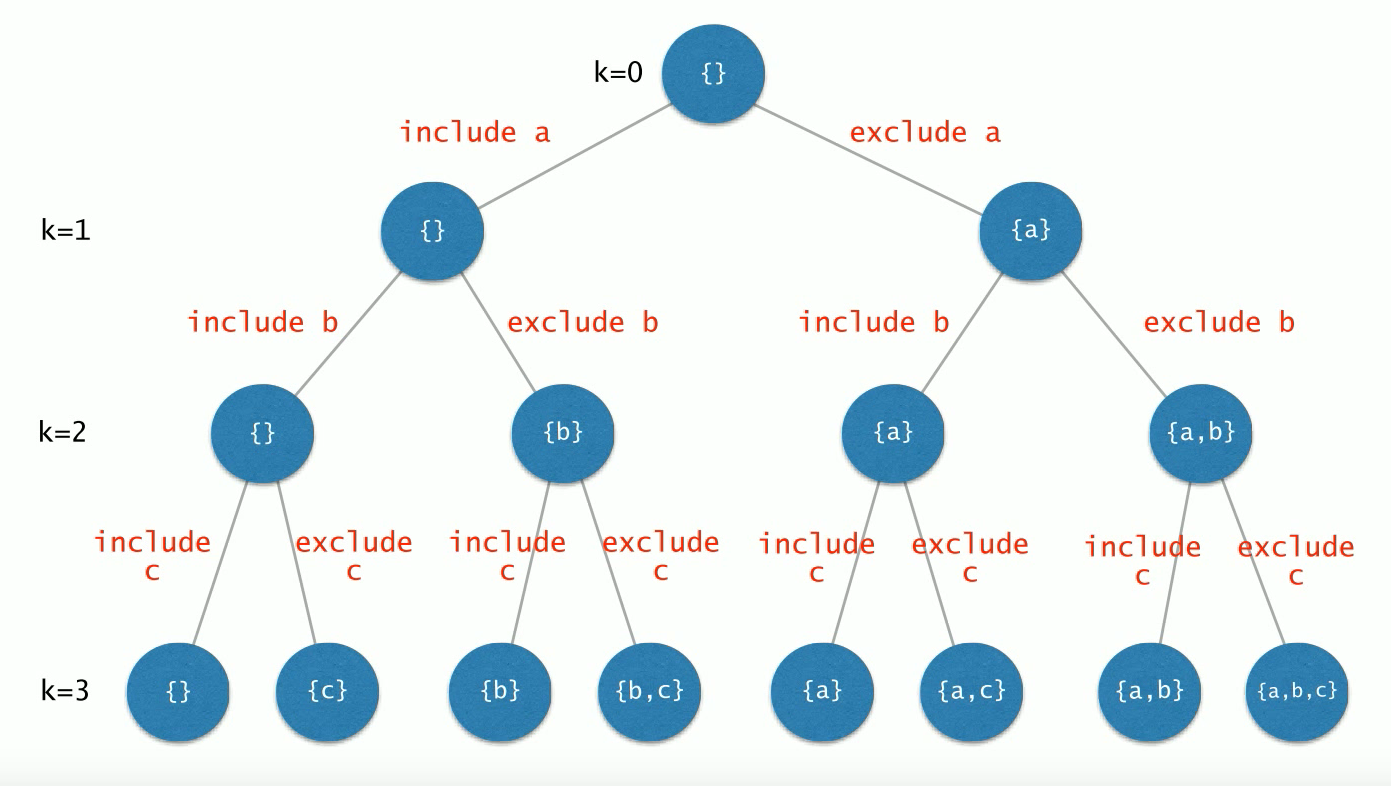
해를 찾기 위해 탐색할 필요가 있는 모든 후보들을 포함하는 트리이다
트리의 모든 노드들을 방문하면 해를 찾을 수 있다.
루트에서 출발하여 체계적으로 모든 노드를 방문하는 절차를 기술한다.
즉, 위의 코드를 상태공간트리의 관점에서 보면
private static char data[] = {'a','b','c','d','e','f'};
private static int n = data.length;
private static boolean[] include = new boolean[n]; //트리상에서 현재 위치를 표현한다
public static void powerSet(int k) { //트리상에서 현재 위치를 표현한다
if (k == n) { //현재 위치가 리프 노드이면 출력하고 끝낸다.
for (int i = 0; i < n; i++)
if (include[i])
System.out.print(data[i] + " ");
System.out.println();
return;
}
//그렇지 않고, 리프노드가 아닌 트리의 어디엔가 위치 한다면
include[k] = false; //트리의 왼쪽노드를 방문한다.
powerSet(k + 1);
include[k] = true; //트리의 오른쪽노드를 방문한다.
powerSet(k + 1);
}상태공간트리의는 이런 방식의 Recursion을 이해하는데 도움을 주는 매우 강력한 도구이며, 앞으로 더 알아갈 것이다.
'ICT Eng > Algorithm' 카테고리의 다른 글
| [Algorithm] 3-2. Merge Sort(합병정렬) (0) | 2018.01.19 |
|---|---|
| [Algorithm] 3-1. 기본 정렬 알고리즘(selection, bubble, insertion sort) with JAVA (1) | 2018.01.17 |
| [Algorithm] 2-6. Recursion 응용 3 - N Queens Problem(Backtracking) (0) | 2018.01.14 |
| [Algorithm] 2-5. Recursion 응용 2 - Counting Cells in a Blob (0) | 2018.01.11 |
| [Algorithm] 2-4. Recursion 응용 1 - 미로찾기 Java 구현 (0) | 2018.01.11 |
- Total
- Today
- Yesterday
- Spring Boot
- IT융합인력양성사업단
- 순환
- Vue.js
- 자바
- vuejs
- 시간복잡도
- 한밭이글스
- Recursion
- Algorithm
- 인프런
- Spring
- 무선통신소프트웨어연구실
- vuex
- 레드블랙트리
- AWS
- springboot
- 젠킨스
- 라즈베리파이
- 정렬
- Raspberry Pi
- 알고리즘
- ORM
- Wisoft
- JPA
- github
- RBT
- 한밭대학교
- Java
- 스프링부트
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
