티스토리 뷰
부경대 IT융합응용공학과 권오흠 교수님의 영리한 프로그래밍을 위한 알고리즘 강좌와 '쉽게 배우는 알고리즘: 관계중심의 사고법 - 문병로'등을 통한 알고리즘 학습 강좌 링크
simple, slow
Bubble sort
Insertion sort
Selection sort
fast
Quick sort
Merge sort
Heap sort
O(n)
Radix sort
분할 정복법 "Divide and Conquer"
merge sort와 quick sort는 분할 정복 알고리즘을 사용한다.
기본적으로 resursion을 사용하여 문제를 해결하는 기법이다.
아래의 세가지 단계를 거쳐서 문제를 해결한다.
분할
해결하고자 하는 문제를 작은 크기의 동일한 문제들로 분할
크기는 작은 사이즈의 문제이지만, 문제 자체는 전체 문제와 동일한 문제들
정복
각각의 작은 문제를 순환적으로 해결
합병
작은 문제의 해를 합하여(merge) 원래 문제에 대한 해를 구함
합병정렬(Merge sort)
divide : 데이터가 저장된 배열을 절반으로 나눔
recursively sort : 각각을 순환적으로 정렬
merge : 정렬된 두 개의 배열을 합쳐 전체를 정렬
주어진 배열을 계속해서 반으로 나누다 보면 결국 길이가 1인 리스트로 쭉 나뉘어진다.
길이가 1인 리스트가 된 순간. 그 각각을 정렬된 리스트로 본다.
이것을 한 단계식 merge하면서 다시 정렬된 리스트를 만드는 방식으로 정렬이 이루어진다.

merge sort에서 가장 중요한 과정이 다음과 같이 merge하는 과정이다. 정렬된 두 배열을 다시 하나의 정렬된 배열로 만드는 과정이다.
정렬 된 두 배열을 합치기 위해, 추가배열을 이용한다.
두개의 리스트에서 두 배열의 첫번째 값 중, 작은 값 하나가 추가배열의 가장 작은 값이 된다.
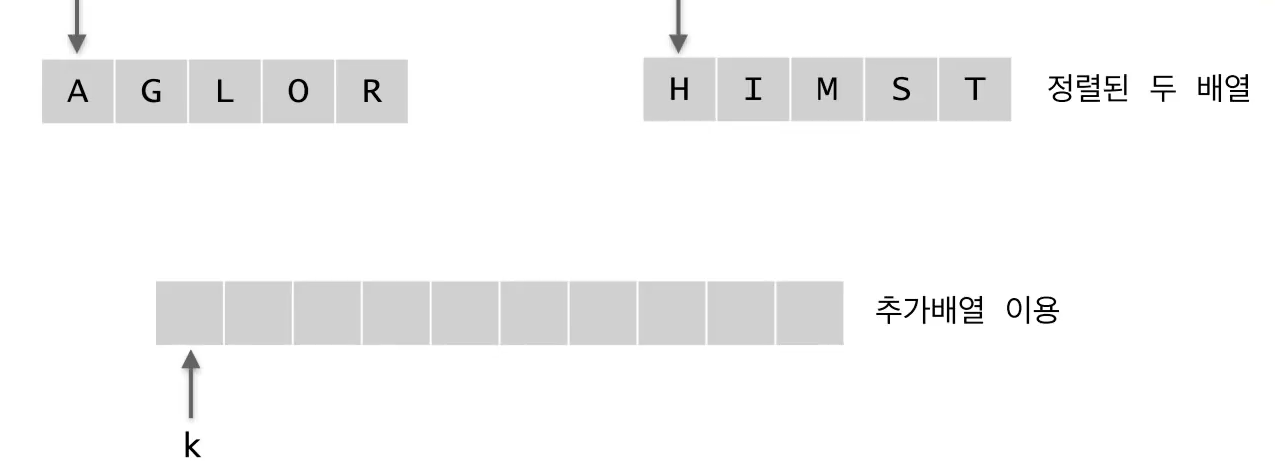
Merge sort Algorithm
recursive한 호출을 하기 위해서 recursion 함수를 기술할 때는, 매개변수를 명시적으로 지정하라.
mergeSort(A[], p, r) {
base case 정의; //p>=r인 경우
if (p < r) then {
q <- (p + q) / 2; //p, q의 중간 지점 계산
mergeSort(A, p, q); //전반부 정렬
mergeSort(A, q+1, r); //후반부 정렬
merge(A, p, q, r); //합병
}
}
merge(A[], p, q, r) {
정렬되어 있는 두 배열 A[p...q]와 A[q+1...r]을 합하여
정렬된 하나의 배열A[p...r]을 만든다.
}실제 merge() 작성
void merge(int[] data, int p, int q, int r) {
int i = p;
int j = q+1;
int k = p;
int[] tmp = new int[data.length];
while (i <= q && j <= r) {
if (data[i] <= data[j])
tmp[k++] = data[i++];
else
tmp[k++] = data[j++];
}
while (i <= q)
tmp[k++] = data[i++];
while (j <= r)
tmp[k++] = data[j++];
for (int i = p; i <= r; i++)
data[i] = tmp[i];
}시간복잡도
n개의 데이터를 정렬하는 시간을 T(n) 이라고 했을 때, N을 반으로 나누어서 정렬하는 시간은 T(n/2)이다. 따라서, 반으로 나눈 배열을 merge sort하는 시간 T(n/2)를 두번 더하고,
다시 이 정렬된 두개의 배열을 merge하는 과정에서 두개의 정렬된 배열의 원소를 한번 비교할 때마다, 정렬된 원소를 저장할 추가 배열에 하나씩 원소가 추가되므로 비교연산의 횟수는 n을 넘지 않는다. 총 원소의 수는 n개이다.
그리고 base case로, 정렬할 데이터가 1개라면 비교 연산의 횟수는 0이다.
따라서 아래와 같이 시간복잡도를 표현할 수 있다.
T(n) =
if n =1
0
otherwise
T(n/2) + T(n/2) + n
=> O(nlogn)
O(nlogn)
길이가 n인 배열을 둘로 쪼개서 다시 정렬된 배열로 병합할 때는 비교의 횟수가 n번을 넘지 않는다.
길이가 n/2인 배열을 정렬하는데에는, n/4의 길이를 가지는 배열 두개를 정렬하므로, 이것의 비교연산 횟수는 n/2이다.
전체로 보면 길이가 n/4인 배열을 두개씩 merge하여 정렬된 n/2배열을 두개 만드는 작업을 수행하는데 드는 비교연산의 횟수는, 2 * (n/2) = n이다.
아래로 내려갈수록 똑같이 비교연산의 횟수는 n이다.
길이가 n인 배열을 길이가 1인 각각의 리스트로 쪼개려면, 아래의 표에서 봤을때 트리의 레벨은 logN이 된다.
따라서, merge sort에 필요한 비교연산의 횟수는 총 n * logn이다.
O(nlogn)

'ICT Eng > Algorithm' 카테고리의 다른 글
| [Algorithm] 3-4. Heap Sort(힙정렬) (2) | 2018.01.24 |
|---|---|
| [Algorithm] 3-3. Quick Sort(빠른정렬) (1) | 2018.01.19 |
| [Algorithm] 3-1. 기본 정렬 알고리즘(selection, bubble, insertion sort) with JAVA (1) | 2018.01.17 |
| [Algorithm] 2-7. Recursion 응용 4 - 멱집합, PowerSet (0) | 2018.01.14 |
| [Algorithm] 2-6. Recursion 응용 3 - N Queens Problem(Backtracking) (0) | 2018.01.14 |
- Total
- Today
- Yesterday
- 인프런
- 시간복잡도
- Java
- 무선통신소프트웨어연구실
- 젠킨스
- AWS
- Spring
- RBT
- 알고리즘
- Raspberry Pi
- IT융합인력양성사업단
- JPA
- vuex
- 정렬
- github
- 순환
- 레드블랙트리
- Algorithm
- springboot
- Wisoft
- 한밭이글스
- 라즈베리파이
- Recursion
- vuejs
- ORM
- Spring Boot
- 스프링부트
- 한밭대학교
- 자바
- Vue.js
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
