티스토리 뷰
[Algorithm] 2-6. Recursion 응용 3 - N Queens Problem(Backtracking)
nroo 2018. 1. 14. 03:24부경대 IT융합응용공학과 권오흠 교수님의 영리한 프로그래밍을 위한 알고리즘 강좌와 '쉽게 배우는 알고리즘: 관계중심의 사고법 - 문병로'등을 통한 알고리즘 학습 강좌 링크
2-6. Recursion의 응용 3 - n queens problem
N-Queens problem(n=8)
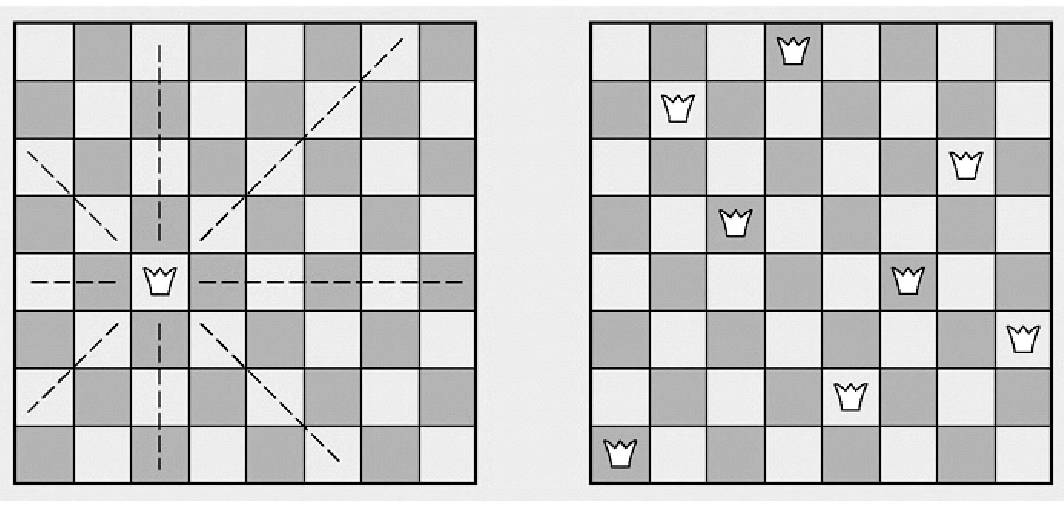
아래의 예(n=8)에서는 8 x 8 체스보드에 8개의 말을 놓는데,
그중에 어떤 말들도 동일한 행, 동일한 열, 동일한 대각선 상에 오지 않도록
n개의 말을 놓을 수 있는가에 대한 문제이다.
위의 방법대로 n개의 말을 놓으려면, 결국 조건을 만족하면서 하나의 행에 하나의 말이 와야한다.
Backtracking
내가 지나온 길을 다시 되돌아 가면서 문제를 해결한다.
어떠한 결정들을 내려가다가, 결정이 막다른 길이다. 즉, 그 결정을 내려서는 안된다 라는것이 분명해지면, 가장 최근에 내렸던 결정을 번복한다.
이런식으로 문제를 해결한다.
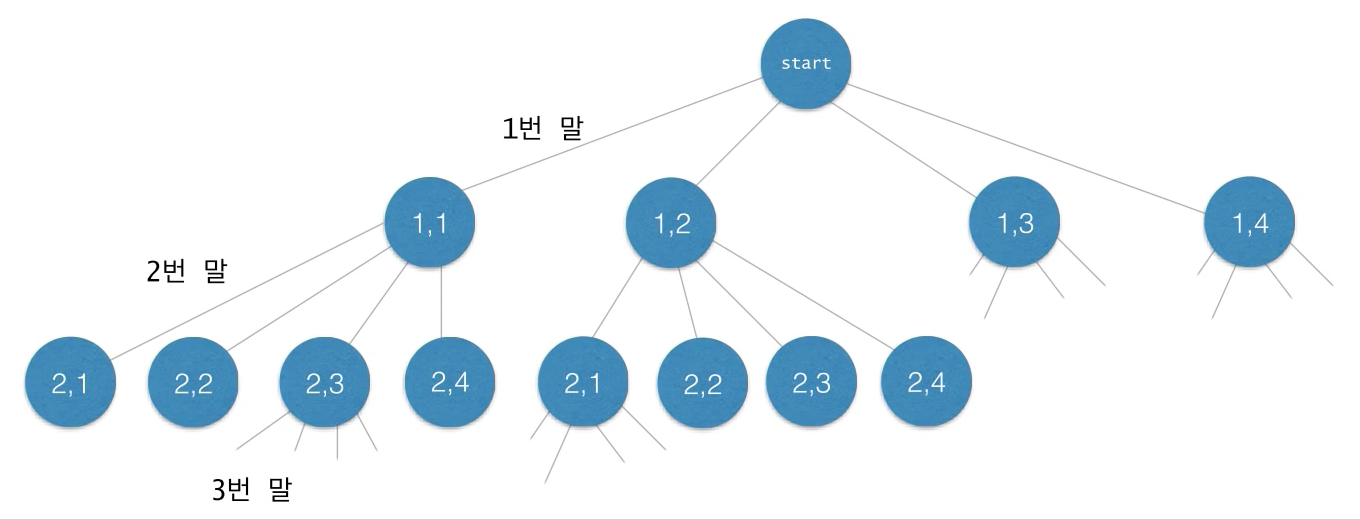
상태공간트리
1번 말이 (1,1)에 위치했을 때, 그리고 그때 2번말이 (2,1), (2,2), (2,3), (2,4)에 위치했을 때, …. 를 나타내는 트리이다.
실제로 완성된 상태공간트리를 그린다면, 4 x 4의 체스보드에 n개의 말을 놓을 수 있는 모든 경우의 수를 나열하는 그림이 될 것이다.
상태공간트리란 찾는 해를 반드시 포함하는 트리이다.
즉, 해가 존재한다면 그것은 반드시 이 트리의 어떤 한 노드에 해당한다.
따라서, 이 트리를 체계적으로 탐색하면 해를 구할 수 있다.
상태공간트리의 모든 노드를 탐색해야 하는 것은 아니다
상태공간트리를 탐색한다는 것은 실제로 모든 트리를 탐색한다는 것이 아니다.
그리고 실제로 트리를 그리거나, datastructure로 만든다는 뜻이 아니다.
상태공간트리는 하나의 개념적인, 논리적인 것이다.
이런 트리를 개념적으로 염두해두고, 실제로는 이 트리의 노드를 탐색하는 코드를 만들면 된다.
Backtracking
상태공간트리를 깊이 우선 방식으로 탐색하여 해를 찾는 알고리즘을 말한다.
알고리즘을 구현하는 방법은 recursion으로 구현하는 방법과 stack을 이용하여 구현하는 방법이 있다.
recursion을 이용하여 구현하는 것이 쉽고, 간명하기 때문에 대부분의 경우 recursion으로 backtracking 알고리즘을 구현한다.

Design Recursion
arguments(매개변수)는 내가 현재 트리의 어떤 노드에 있는지를 지정해야 한다.
즉, 상태공간트리에서 어떤 노드에 도착했다. 를 나타내야 한다.
그리고 이 함수에서 수행할 코드는 어떤 노드에 도착했을때, 그 이후에 행해져야할 작업들이다.
if -> 제일 먼저 할 것은 이 노드가 non-promising 또는 infeasible한 노드인지를 판단한다. 즉, 해당 노드의 아래 깊이를 더 탐색해볼 가치가 있는 노드인가를 판단한다. 아니라면 되돌아간다.
else if -> 그렇지 않다면, 어떤 노드에 도착했는데 답을 찾은 경우라면, 답을 출력하고 return 한다.
else if -> 그렇지 않다면, 그 노드가 실패도 아니고 답도 아니라면, 해야 할 일은 해당 노드의 자식들을 순서대로 방문해보는 것이다. recursive하게.
Backtracking을 구현하는 대부분의 함수들은 기본적으로 이런 구조를 가진다.
return-type queens(arguments) {
if non-promising
report failure and return;
else if success
report answer and return;
else
visit children recursively;
}매개변수와 전역변수를 유지함으로써 현재 어떤 노드에 위치하고 있는지를 나타낸다.
매개변수 level은 현재노드의 level을 표현하고, i번에서 level번째말이 어디에 놓였는지는 전역변수 배열 cols로 표현한다. cols[i]=j는 i번 말이 (i행, j열)에 놓였음을 의미한다.
return type은 boolean으로 성공이냐 실패냐를 반환한다.
non-promising여부를 판단하는 함수를 만들었다고 가정하고, 검증 후 false를 리턴한다.
int[] cols = new int[N+1];
boolean queens(int level) {
if (!promising(level)))
return false;
else if success
report answer and return;
else
visit children recursively;
}promising 검증을 통과했다는 가정(이 말은 현재까지 놓인 말들이 충돌 없이 잘 놓여졌다는 의미이다.)하에 level==N이면 모든 말이 놓였다는 의미이고 따라서 성공이다.
int[] cols = new int[N+1];
boolean queens(int level) {
if (!promising(level)))
return false;
else if (level==N)
return true;
else
visit children recursively;
}마지막으로 자식노드들을 recursive하게 방문하는 코드이다.
이 때는, 1번 말부터 level번째 말까지 잘 놓였다는 의미이고 따라서 level+1번째 말을 1열과 N열 사이에서 어느 곳에 놓아야 하는 가에 대한 고민을 해야한다. N가지 선택 가능한 경로가 있다.
level+1번째 말을 각각의 열에 놓은 후 recursion을 호출한다.
코드에서 보면 level+1번의 말을 i에 놓아보고 queens(level+1)을 호출한다. 이것이 true라면 true를 리턴하고, 실패라면 다시 돌아가서 i+1번째 열에 놓고 다시 검증한다.
int[] cols = new int[N+1];
boolean queens(int level) {
if (!promising(level)))
return false;
else if (level==N)
return true;
for (int i = 1; i <= N; i++) {
cols[level + 1] = i;
if(queens(level+1))
return true;
}
return false;
}Promising Test를 어떻게 할 것인가
위의 코드에서 보면 queens()메소드를 호출할 때 마다 promising 여부를 검증하고 있다. 따라서 cols[]의 1,2,3에 해당하는 말들 간에는 충돌이 없다고 보장되어 있다.
따라서 마지막에 놓인(cols[4]) 이 말이 이전에 놓인 다른 말들과 충돌하는지 검사하는 것으로 충분하다.

코드는 다음과 같은 방식으로 작성한다.
같은 열에 놓였는지,
cols[i] == cols[level]
동일 대각선상에 놓였는지를 검사한다.
(level - i) == Math.abs(cols[level] - cols[i])
boolean promising(int level) {
for (int i = 1; i < level; i++) {
if (cols[i] == cols[level])
return false;
else if ((level - i) == Math.abs(cols[level] - cols[i]))
return false;
}
return true;
}정리
말이 놓인 위치 출력
첫 호출은 quuens(0)
public class NQueensProblem {
private final static int N = 8;
private static int[] cols = new int[N + 1];
public static void main(String[] args) {
queens(0);
}
private static boolean queens(int level) {
if (!promising(level))
return false;
else if (level == N) {
for (int i = 1; i <= N; i++)
System.out.println("(" + i + ", " + cols[i] + ")");
return true;
}
for (int i = 1; i <= N; i++) {
cols[level + 1] = i;
if (queens(level + 1))
return true;
}
return false;
}
private static boolean promising(int level) {
for (int i = 1; i < level; i++) {
if (cols[i] == cols[level])
return false;
else if ((level - i) == Math.abs(cols[level] - cols[i]))
return false;
}
return true;
}
}
(1, 1)
(2, 5)
(3, 8)
(4, 6)
(5, 3)
(6, 7)
(7, 2)
(8, 4)
Process finished with exit code 0'ICT Eng > Algorithm' 카테고리의 다른 글
| [Algorithm] 3-1. 기본 정렬 알고리즘(selection, bubble, insertion sort) with JAVA (1) | 2018.01.17 |
|---|---|
| [Algorithm] 2-7. Recursion 응용 4 - 멱집합, PowerSet (0) | 2018.01.14 |
| [Algorithm] 2-5. Recursion 응용 2 - Counting Cells in a Blob (0) | 2018.01.11 |
| [Algorithm] 2-4. Recursion 응용 1 - 미로찾기 Java 구현 (0) | 2018.01.11 |
| [Algorithm] 2-3. 순환의 개념과 기본 3 - Designing Recursion (0) | 2018.01.09 |
- Total
- Today
- Yesterday
- vuex
- Recursion
- Spring
- Java
- 레드블랙트리
- 자바
- IT융합인력양성사업단
- springboot
- Raspberry Pi
- 무선통신소프트웨어연구실
- Spring Boot
- 알고리즘
- Vue.js
- 한밭이글스
- ORM
- 라즈베리파이
- RBT
- github
- Algorithm
- 시간복잡도
- JPA
- 젠킨스
- 스프링부트
- 인프런
- 한밭대학교
- vuejs
- AWS
- 정렬
- Wisoft
- 순환
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
