티스토리 뷰
부경대 IT융합응용공학과 권오흠 교수님의 영리한 프로그래밍을 위한 알고리즘 강좌와 '쉽게 배우는 알고리즘: 관계중심의 사고법 - 문병로'등을 통한 알고리즘 학습 강좌 링크
3-6. 정렬의 하한(lower bound)
Comparison Sort
O(n²)
bubble sort
selection sort
insertion sort
quick sort(최악의 경우. 평균은 O(nlogn))
O(nlogn)
merge sort
heap sort
O(nlogn)보다 시간복잡도가 더 낮은 comparison 정렬 알고리즘은 존재할 수 없다는 것이 이번 학습에서 얻을 수 있는 결론이다.
정렬 알고리즘의 유형
Comparison sort
데이터들간의 상대적 크기관계만을 이용해서 정렬하는 알고리즘
따라서 데이터들간의 크기 관계가 정의되어 있으면 어떤 데이터에든 적용가능 (문자열, 알파벳, 사용자 정의 객체 등)
버블정렬, 삽입정렬, 합병정렬, 퀵정렬, 힙정렬 등
Non-comparison sort
정렬할 데이터에 대한 사전지식을 이용 - 적용에 제한
ex) 내가 정렬할 데이터가 두자리 수 정수다 라는 것을 알고 있는 상태에서, 90점대, 80점대, 70점대 의 점수로 분류하는 것
Bucket sort
Radix sort
정렬문제의 하한
결론
어떤 comparison sort도 시간복잡도가 O(nlogn)보다 낮을 수는 없다.
하한 (Lower bound)
입력된 데이터를 한번씩 다 보기위해서 최소 Θ(n)의 시간복잡도 필요
합병정렬과 힙정렬 알고리즘들의 시간복잡도는 Θ(nlogn)
어떤 comparison sort알고리즘도 Θ(nlogn)보다 나을 수 없다.
Comparison sort의 시간복잡도를 증명하기 위해 decision tree라는 도구를 사용한다.
Decision Tree
임의의 comparison sort가 있다고 가정하자. (여기서는 insertion sort)
정렬을 하기 위해 값들을 하나씩 비교하는 전체과정을 하나의 트리로 나타낼 수 있다.
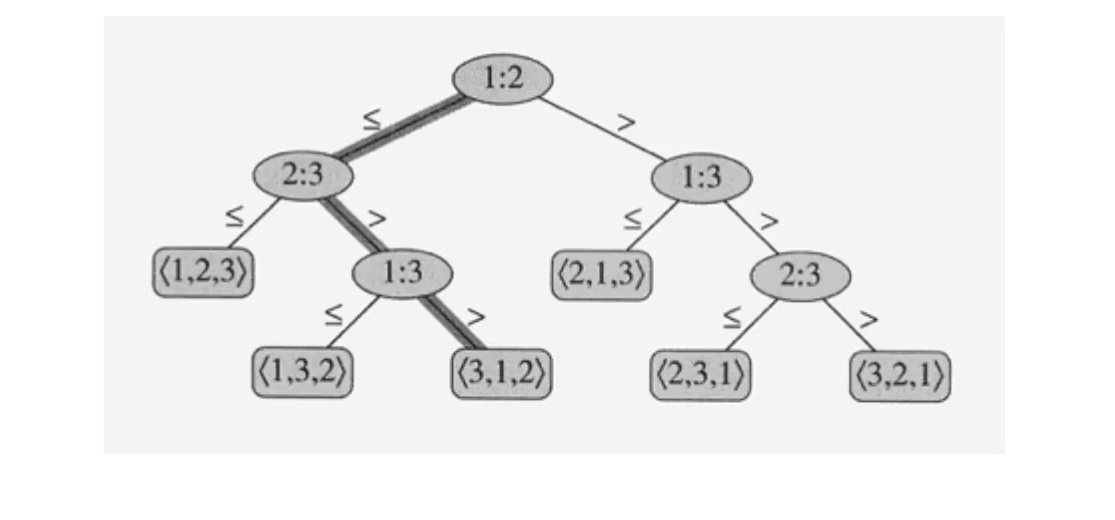
3개의 값을 정렬하는 삽입 알고리즘에 대한 decision tree
정렬의 결과는 left node에 나타나며, 갯수는 n!이다. 모든 순열(permutation)에 해당하기 때문이다.
최악의 경우 시간복잡도는 decision tree의 높이
트리의 높이는
height >= logn! = Θ(nlogn)
comparison sort 알고리즘을 decision tree로 표현하게 되면, 해당 decision tree는 leaf노드를 n!개 가져야 한다.
그런데, 어떤 이진 트리의 leaf노드가 n!개를 가지려면 그 트리의 높이는 log n! 보다 더 낮을 수는 없다.
logn!을 수학적으로 증명하게 되면(stirling's formula 참고), Θ(nlogn)이 된다.
따라서, 어떤 comparison sort던 decision tree의 높이가 Θ(nlogn)보다 낮을 수는 없음을 증명한 것이 된다.
정리
'ICT Eng > Algorithm' 카테고리의 다른 글
| [Algorithm] 3-8. Radix Sort (0) | 2018.01.31 |
|---|---|
| [Algorithm] 3-7. Counting Sort - 선형시간 알고리즘 (0) | 2018.01.29 |
| [Algorithm] 3-5. 우선순위 큐(priority queue) (0) | 2018.01.26 |
| [Algorithm] 3-4. Heap Sort(힙정렬) (2) | 2018.01.24 |
| [Algorithm] 3-3. Quick Sort(빠른정렬) (1) | 2018.01.19 |
- Total
- Today
- Yesterday
- Spring
- Algorithm
- 시간복잡도
- JPA
- 한밭이글스
- IT융합인력양성사업단
- Recursion
- springboot
- 젠킨스
- 레드블랙트리
- AWS
- Wisoft
- 알고리즘
- ORM
- 라즈베리파이
- github
- 인프런
- 자바
- Java
- Vue.js
- Raspberry Pi
- vuejs
- Spring Boot
- 순환
- 스프링부트
- 무선통신소프트웨어연구실
- vuex
- 한밭대학교
- RBT
- 정렬
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
